Activer le mode zen
Ressource au format PDF
Mots-clés
gravitation ellipsoïde de référence géoïde force de Coriolis force d'entrainement pesanteurClassification
Le Mississippi coule-t'il "vers le haut" ? Quelques précisions sur la gravité à la surface de la Terre
15/12/2003
Résumé
Un article sur la gravité, la pesanteur à la surface de la Terre, le géoïde.
Table des matières
- La gravité en première approximation
- "E pur, si muove..."
- La pesanteur à la surface de la Terre : un sujet qui n'est pas si simple que
cela...
- La verticale, le "haut" et le "bas"
- La verticale : la direction du fil à plomb
- L'horizontale : une surface bosselée aussi appelée "équipotentielle de pesanteur"
- Inhomogénéités de la Terre
- Est-ce que le géoïde coïncide avec la surface moyenne des océans ?
- Qu'est-ce que le "haut" et le "bas" ?
- La pesanteur est-elle constante sur une horizontale ?
- Application au cours du Mississippi
- La verticale, le "haut" et le "bas"
- Conclusion
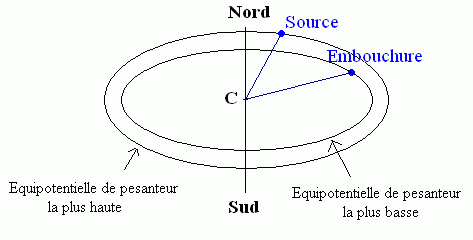
La source du Mississippi est plus proche (de 5 kilomètres!) du centre de la Terre que son embouchure. Ce n'est pas une plaisanterie, ni un "miracle", mais une conséquence naturelle des lois de la gravité.
Figure 1. Le fleuve Mississippi
La gravité en première approximation
En première approximation, on représente la Terre comme une sphère parfaite homogène et immobile. Cette sphère "idéale" attire alors vers son centre tout objet présent à sa surface. La verticale en un point est donnée par la direction du fil à plomb qui, dans cette représentation simplifiée, coïncide avec la droite passant par ce point et par le centre de la Terre. Dans cette approximation, le poids P d'un objet à "l'altitude 0" sur Terre est le même en tout point, et est donné par P = m g0 où m est la masse de l'objet et g0 = 9,8N/kg, l'intensité de la pesanteur, est la même en tout point d'altitude 0. Le poids d'un objet donné ne dépend alors que de son altitude*. |  Figure 2. la Terre comme une sphère "idéale" |
Le poids d'un objet de masse m à l'altitude h est donné, dans cette approximation, par l'expression : F = m g0 R2/(R + h)2 où R représente le rayon de la Terre : R = 6,4 × 106 m environ.
"E pur, si muove..."
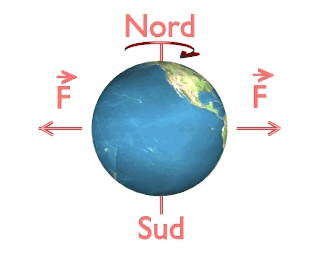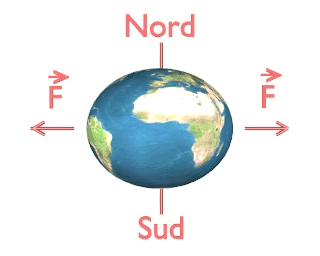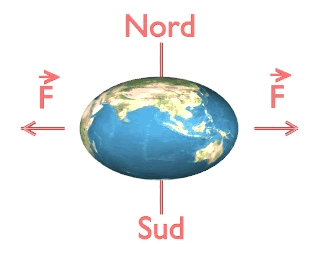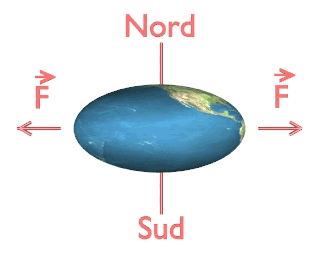
Conséquences de la rotation de la Terre sur sa forme
La Terre est aplatie aux pôles et renflée à l'équateur. Son rayon aux pôles est de 6356,754 km et son rayon à l'équateur vaut : Re = 6378,139 km, soit une différence de 21 km environ entre les deux.
Cet aplatissement est dû à la rotation de la Terre autour de son axe. On a représenté dans l'animation ci-dessous l'aplatissement de la Terre sous l'effet de sa rotation. Bien évidemment, par rapport au rayon de la Terre, son aplatissement représente moins d'un trois millième de son rayon, c'est donc un effet qui serait totalement imperceptible sur un schéma à l'échelle. L'aplatissement représenté sur l'animation est par conséquent très exagéré.
Un objet en rotation autour d'un axe a tendance à s'éloigner de ce dernier. Il subit l'effet des "forces" centrifuges (notées F sur l'animation) qui tendent à l'éloigner de l'axe. Si on modélise la Terre comme une sphère "fluide" en rotation autour de l'axe des pôles, cette dernière va, sous l'action des forces centrifuges, prendre une forme d'ellipsoïde aplati
Cet aplatissement de la Terre a été prédit dès le XVIIième siècle par Newton (en 1687 précisément). Il fut vérifié lors de deux expéditions, l'une près du pôle, dans le Golfe de Botnie, en Finlande, par Maupertuis et Celsius, l'autre près de l'équateur, au Pérou, par Godin, La Condamine, Bouguer, de Jussieu et leurs compagnons de voyage...
Les voyageurs sont revenus (pour ceux qui en sont revenu!) après avoir vérifié qu'un degré de méridien est plus long au pôle qu'à l'équateur... Ces voyages n'étaient pas une mince affaire : si le voyage en Laponie a été relativement aisé (1736-1737), celui du Pérou, commencé en 1735, a duré 9 ans...
La Terre n'est pourtant pas un fluide !
Si l'on conçoit bien comment la forme d'une sphère fluide peut avoir été influencée par son mouvement de rotation, on peut avoir du mal à imaginer un rocher, par exemple, être déformé sous l'effet des forces centrifuges.
Or, la Terre, telle que nous la percevons à notre échelle de temps, se comporte comme un solide et non comme un fluide. En fait, si l'on s'intéresse aux valeurs numériques des coefficients de viscosité, on constate que le manteau Terrestre est même extrêmement rigide, bien plus que la glace, pour prendre un exemple de solide que nous rencontrons dans la vie courante : une estimation de la viscosité du manteau donne 1021Pa.s alors que celle d'un glaçon à 0°C est de l'ordre de 1010 Pa.s et celle de l'eau à l'état liquide est de l'ordre de 10-3 Pa.s.
Comment expliquer alors la déformation de la Terre sous l'effet de sa rotation?
La réponse tient à l'échelle de temps considérée : solide à l'échelle humaine, le manteau terrestre est fluide à l'échelle des temps géologiques.
Et le Mississippi ?
La première explication qui vient à l'esprit est que le Mississippi, entre sa source et son embouchure, s'est significativement rapproché de l'équateur... Or, le pôle est plus proche du centre de la Terre que l'équateur, ceci explique que la source du Mississippi puisse être plus près du centre de notre planète que son embouchure...
Cette explication semble raisonnable, mais soulève d'autres questions :
le Mississippi coule-t'il donc "vers le haut" ?
Qu'appelle-t'on "haut" et "bas" ?
L'intensité de la pesanteur est plus forte à la source du Mississippi (plus proche du centre de la Terre) qu'à son embouchure, est-ce normal ?
La pesanteur à la surface de la Terre : un sujet qui n'est pas si simple que cela...
La verticale, le "haut" et le "bas"
La verticale : la direction du fil à plomb
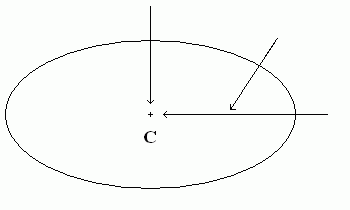
La verticale en un point donné de la surface de la Terre est la direction du fil à plomb en ce point. Cette direction dépend du lieu, et n'est dirigée vers le centre de la Terre qu'en première approximation. |  Toutes les verticales (représentées par des flèches) ne concourent pas au centre C de la Terre (représentée ici, pour mieux illustrer le problème, comme exagérément aplatie) |
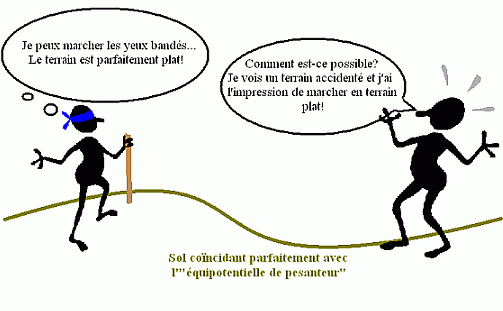
Si la surface de la Terre était recouverte d'eau en équilibre, la direction du fil à plomb serait constamment perpendiculaire à la surface de l'eau.
L'horizontale : une surface bosselée aussi appelée "équipotentielle de pesanteur"
On appelle "horizontale" toute surface perpendiculaire en tout point à la verticale. Cette surface est aussi une équipotentielle de pesanteur, c'est-à-dire une surface sur laquelle le potentiel de pesanteur (qui inclut le potentiel gravitationnel mais aussi les forces centrifuges et de marée) est constant.
En fait, l'effet des marées n'est pas constant dans le temps, donc en toute rigueur l'équipotentielle ainsi définie n'est pas rigoureusement fixe mais en pratique on appelle "équipotentielle de pesanteur" la valeur moyenne de cette surface.
L'équipotentielle de pesanteur particulière correspondant avec le niveau des océans tels qu'il serait s'ils étaient immobiles (donc en supprimant la houle, les courants marins, etc...) est appelée "géoïde".
En toute première approximation, le géoïde est une sphère, en deuxième approximation il s'agit d'un ellipsoïde, que l'on appelle "l'ellipsoïde de référence", en toue rigueur il ne s'agit ni d'un ellipsoïde, ni même d'une surface de révolution, comme nous allons le voir dans la partie suivante.
Inhomogénéités de la Terre
Si l'on veut obtenir la forme véritable des équipotentielles de pesanteur terrestres, il faut tenir compte des forces centrifuges et de toutes les forces de gravitation, celles-ci dépendant non seulement des irrégularités de la surface terrestre mais aussi des inhomogénéités en profondeur des matériaux dont la Terre est composée.
C'est ainsi qu'en observant la surface de la mer par satellites que l'on peut se faire une idée des montagnes sous-marines existant à cet endroit : on constate des irrégularités persistantes de la surface de l'eau, ces irrégularités sont, pour certaines, dues au relief du fond des mers, et pour d'autres à des inhomogénéités présentes dans le manteau de la Terre (ces irrégularités peuvent faire jusqu'à une centaine de mètres).
Ces reliefs sous-marins ne sont pas sensibles pour la personne qui se trouve à la surface car cette personne est soumise au même champ de gravitation que la surface de l'eau, et la force de pesanteur reste constamment perpendiculaire à cette surface (dans le cas d'une surface idéale immobile de température constante).
Situation imaginaire dans laquelle la surface du sol irrégulière représentée ci-dessus correspondrait à une équipotentielle de pesanteur locale
Figure 5. Équipotentielle de pesanteur locale
Est-ce que le géoïde coïncide avec la surface moyenne des océans ?
La réponse est... presque oui, mais pas tout à fait...
En fait, il y a quelques mètres de différence. Cette différence vient du fait que l'équipotentielle de pesanteur tient en compte les forces de gravitation et la force centrifuge, mais que l'océan est aussi parcouru par des courants marins permanents, comme le Gulf Stream, qui subissent l'effet des forces de Coriolis, et qu'il y a aussi quelques inhomogénéités de température... qui persistent même une fois la surface des océans moyennée sur le temps. Cette différence reste cependant minime.
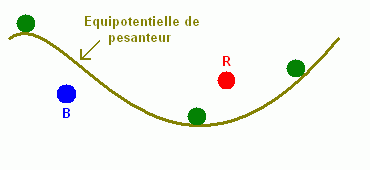
Qu'est-ce que le "haut" et le "bas" ?
Le "haut" et le "bas" pour un individu situé sur une équipotentielle de pesanteur donnée sont définis par la position des objets par rapport à cette équipotentielle. Les objets situés exactement sur l'équipotentielle de cette personne ne sont, ni plus hauts, ni plus bas que celle-ci, bien que la surface de cette équipotentielle soit plus proche d'un ellipsoïde bosselé que d'une sphère et que ces objets ne soient pas tous situés à la même distance du centre de la Terre.
Les billes vertes sont toutes situées à la même altitude, la bille bleue B est plus basse, et la bille rouge R est plus haute
Figure 6. Équipotentielle de pesanteur
La pesanteur est-elle constante sur une horizontale ?
La réponse doit maintenant sembler claire : la force de pesanteur n'a pas de raison d'être constante sur une horizontale. Une horizontale, par définition, est une surface où le potentiel de pesanteur est constant, et il n'y a pas de lien entre constance du potentiel et constance de la force.*
Il est de même tout à fait normal que la force de gravitation soit plus intense à la source du Mississippi (plus proche du centre de la Terre, quoique plus haute) qu'à son embouchure (plus éloignée du centre de la Terre, quoique plus basse).
On peut illustrer la différence entre potentiel et force (qui est, mathématiquement parlant, le gradient, donc une dérivée, du potentiel) en faisant une analogie avec des courbes de niveau : la pente (gradient d'altitude) n'est pas la même en tout point d'une courbe de niveau (qui correspond à une altitude constante).
Application au cours du Mississippi
Il y a 21 kilomètres de différence entre le rayon au pôle Nord et celui à l'équateur, donc deux points peuvent se trouver à la même altitude bien qu'il y ait des kilomètres de différence entre leurs distances respectives au centre de la Terre.
De même, bien que la source d'un fleuve soit plus haute que son embouchure, ceci ne permet pas de conclure quoi que ce soit sur les distances de la source et de l'embouchure au centre de la Terre.
Si on imagine, par exemple, un fleuve qui coulerait du Pôle à l'équateur, sa source pourrait être jusqu'à 21 kilomètres plus haute que son embouchure et malgré tout être plus proche du centre de la Terre.
La source d'un fleuve peut être plus proche du centre de la Terre que son embouchure, bien qu'elle appartienne à l'équipotentielle de pesanteur la plus haute (les échelles n'ont pas été respectées sur cette image)
Le cas du Mississippi, quoique pas aussi extrême que cet exemple imaginaire, illustre bien la différence qui existe entre "altitude" et "distance au centre de la Terre" : le Mississippi ne coule pas "vers le haut" mais "vers un point plus éloigné du centre de la Terre", de plus, si la pesanteur est plus intense à sa source qu'à son embouchure, le fleuve coule bien d'un point dont le potentiel de pesanteur est plus élevé vers un point dont le potentiel de pesanteur est plus faible.
Conclusion
Il convient de bien différencier l'altitude d'un point (qui est 0 si le point se trouve sur le géoïde, surface irrégulière qui n'assume la forme d'une sphère qu'en première approximation) de sa distance au centre de la Terre. La forme du géoïde est très complexe et est le résultat des forces centrifuges, des irrégularités et des inhomogénéités de la Terre ainsi que de la valeur moyenne des forces de marée.
D'autre part, si une équipotentielle de pesanteur correspond effectivement à un potentiel de pesanteur constant, la force de pesanteur, elle, n'est pas constante sur cette surface. Un des exemples les plus frappants est peut-être la différence de gravité qui existe entre le Pôle et un point du géoïde qui serait situé sur l'équateur terrestre : bien que ces deux points soient à la même altitude, les valeurs de g sont différentes. Il faut donc veiller à ne pas confondre force et potentiel !...
Pour citer cet article :
Le Mississippi coule-t'il "vers le haut" ? Quelques précisions sur la gravité à la surface de la Terre, Gabrielle Bonnet, décembre 2003. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Mississippi.xml
