Activer le mode zen
Ressource au format PDF
Mots-clés
- Lune
- trajectoire
- orbite
- ellipse
- apogée
- chiffres significatifs
- excentricité
- ligne des noeuds
Classification
Perturbations de la trajectoire de la Lune
14/09/2004
Résumé
Cet article met en évidence et explique la complexité du mouvement de la Lune, et à travers l'exemple du périmètre de l'orbite lunaire, illustre le problème général du choix du nombre de chiffres significatifs.
Table des matières
Nous avons récemment reçu une affirmation au sujet de la distance parcourue par la Lune sur son orbite, faisant état de 8 chiffres significatifs...
Au-delà du problème précis abordé, se pose la question de la pertinence de l'expression : "la distance parcourue par la Lune sur son orbite est (suivi d'un résultat avec un très grand nombre de chiffres significatifs)". En effet, cette distance est-elle tellement constante que l'on puisse la donner avec une si grande précision ?
Le but de cet article est double : mettre en évidence la complexité du mouvement de la Lune et comprendre l'origine de cette complexité, et à travers cette compréhension, illustrer le problème général en physique du choix du nombre de chiffres significatifs sur l'exemple du périmètre de l'orbite lunaire, puisque c'est cet exemple qui a été abordé lors d'une question.
Comment calculer la valeur de la distance D parcourue par la Lune sur son orbite à un moment donné ?
La recherche de précision sur un calcul simple comme celui-ci va nous amener à étudier la complexité du mouvement de la Lune...
La trajectoire de la Lune assimilée à un cercle ?
Le calcul le plus simple de la distance parcourue par la Lune sur son orbite consiste à prendre la distance moyenne Rm entre la Terre et la Lune (on trouve par exemple dans un livre la valeur Rm = 384 400 km environ), et à considérer que la trajectoire de la Lune, en première approximation, est un cercle.
Ceci nous donne (provisoirement du moins) :
distance D parcourue par la Lune sur son orbite = 2 π Rm ≃ 2,415 × 109 m |
Ce calcul appelle quelques commentaires. Il peut être légitime, selon le nombre de chiffres significatifs que l'on souhaite obtenir sur le résultat final, d'approcher la trajectoire de la Lune par un cercle, mais est-il raisonnable dans ce cas de garder 4 chiffres significatifs?
Quelle approximation a-t'on faite en considérant l'orbite de la Lune comme un cercle?
Première estimation de l'erreur commise en assimilant la trajectoire de la Lune à un cercle :
La véritable trajectoire de la Lune est plus proche d'une ellipse que d'un cercle. Supposons-la pour l'instant parfaitement elliptique. On peut trouver les extrema de la distance Terre-Lune dans un livre : dans le livre que je consulte, je trouve 363 300 km environ au périgée et 405 500 km environ lorsque la Lune est à son apogée...
On peut alors calculer un encadrement grossier pour la distance D parcourue par la Lune sur son orbite en prenant la distance maximale de la Terre à la Lune, et en multipliant par 2 π, et faire de même pour la valeur minimale :
2,28 × 109 m < D < 2,55 × 109 m |
par suite nous avons une idée de l'erreur que nous avons pu commettre avec notre premier calcul : le premier chiffre de notre calcul précédent semble sûr, la première décimale déjà est plus incertaine... Au-delà, donner le résultat de notre calcul avec plus de décimales est illusoire.
On peut argumenter, cependant, que ceci n'est qu'un encadrement très grossier de l'erreur. En effet, l'erreur réelle est probablement inférieure à cette valeur, puisque la Lune est tantôt plus loin, tantôt moins loin de la Terre que la valeur donnée par le rayon moyen : les erreurs ont tendance à se compenser.
Nous allons donner une valeur plus précise de l'erreur commise en assimilant la trajectoire de la Lune à une ellipse parfaite et en calculant le périmètre de cette ellipse.
Périmètre de l'ellipse lunaire
Comment trouver le périmètre de l'ellipse lunaire si on dispose des valeurs de la distance Terre-Lune au périgée et à l'apogée?
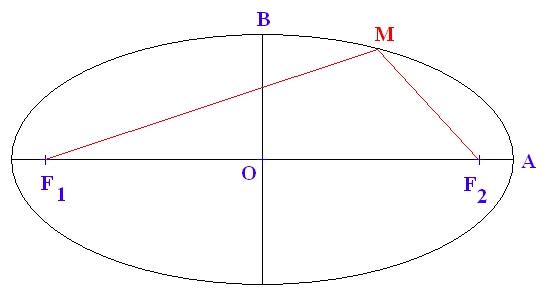
Figure 1. Calcul du périmètre d'une ellipse
Si O est le centre de l'ellipse, OA = a le demi-grand axe de l'ellipse, OB = b le demi-petit axe, F1 et F2 les deux foyers de l'ellipse, et si on note OF1 = OF2 = c, alors on a :
a2 = b2 + c2 |
En fait, F1M + MF2 = 2 a quel que soit le point M sur l'ellipse. Appliquée au point B, cette relation permet de démontrer la relation ci-dessus entre a, b, et c.
l'excentricité e, qui définit l'écart de l'ellipse à un cercle parfait vaut
e = c/a (e = 0 dans le cas d'un cercle) |
Comment calculer le périmètre d'une ellipse?
Le périmètre P d'une ellipse de demi-grand axe a et d'excentricité e peut être mis sous la forme :
P = 4 a ∫0π/2 (1 - e2 sin2 θ)1/2 dθ |
Calcul du périmètre de l'orbite lunaire
Pour calculer le périmètre de l'orbite lunaire à partir de la formule précédente, il suffit de connaître les valeurs de a et de e. Cependant, si l'on recherche une bonne précision sur le résultat (de l'ordre du % ou plus), on ne peut pas assimiler le foyer de l'orbite lunaire à la Terre. En effet, le foyer de cette orbite, rigoureusement parlant, est le centre de gravité du système Terre-Lune. Comme la Terre a une masse qui est à peu près 100 fois celle de la Lune, assimiler le foyer de l'ellipse à la Terre entraîne une erreur de l'ordre du % sur le résultat.
La masse de la Terre vaut MT = 5,98 × 1024 kg et la masse de la Lune vaut ML = 7,35 × 1022 kg, par conséquent, la distance maximale a + c du foyer de l'ellipse (= centre de gravité du système Terre-Lune) à la Lune vaut :
MT/(MT + ML) × distance maximale Terre-Lune soit 4,01 × 108 m
On calcule de même la distance minimale du foyer de l'ellipse à la Lune (correspondant à a - c), et on trouve 3,59 × 108 m, donc a = 3,80 × 108 m, c = 2,1× 107 m et e = 0,055
Un calcul numérique de P donne P = 2,39 × 109 m. Si on compare cette valeur à la valeur obtenue en assimilant la trajectoire de la Lune à un cercle de rayon Rm on trouve que la différence est de l'ordre de 1%. Le résultat du 1.1. avait donc, si on se fie à ce calcul, 2 chiffres significatifs.
En fait le résultat que nous avons trouvé ici est lui-même entaché d'erreur car la trajectoire de la Lune n'est pas rigoureusement une ellipse fixe dans le référentiel géocentrique. Nous allons nous pencher maintenant sur ces variations de l'orbite de la Lune et sur leur origine.
La trajectoire de la Lune varie beaucoup plus que celle de la Terre...
Une trajectoire complexe
La Lune a une trajectoire complexe, sujette à de nombreuses variations, dont nous allons résumer les principales.
La trajectoire de la Lune est sujette à des variations périodiques :
- Variation de l'excentricité de l'ellipse de la Lune, sur une période de 421 jours, entre 0,044 et 0,067 environ. Dans le même temps, le grand axe de l'orbite lunaire oscille lui aussi (amplitude maximale d'une douzaine de degrés).
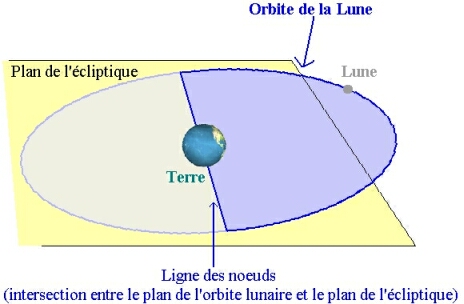
- Rotation de la ligne des noeuds qui effectue un tour complet en 18,61 ans
- Rotation du demi grand axe dans le plan de la trajectoire de la Lune, de période 8,85 années
- variation périodique de l'inclinaison du plan de l'orbite de la Lune par rapport au plan de l'écliptique, qui varie entre 5° et 5°18' en 173 jours
De plus, la Lune s'éloigne petit à petit de la Terre, de quelques centimètres par an (4,4 ± 0,6 cm/an)...
Quelle est l'incidence de ces variations sur les paramètres de l'orbite lunaire (et entre autres choses son périmètre) ?
En fait, les distances données sont soit des valeurs moyennes, soit des valeurs prises à un instant donné : les variations de l'orbite de la Lune sont telles que si on regarde les derniers mois (juillet 2004 à septembre 2004), on trouve :
- périgée le premier juillet, distance Terre-Lune : 357 448 km
- apogée le 14 juillet, distance Terre-Lune : 406 192 km
- périgée le 30 juillet, distance Terre-Lune : 360 324 km
- apogée le 11 août, distance Terre-Lune : 405 292 km
- périgée le 27 août, distance Terre-Lune : 365 105 km
- apogée le 8 septembre, distance Terre-Lune : 404 464 km
- périgée le 22 septembre, distance Terre-Lune : 369 589 km
Au cours de 3 mois, le périgée varie d'à peu près 3% et l'apogée de 0,4% environ... Les incertitudes correspondantes sur la valeur du périmètre de l'orbite lunaire sont de l'ordre du %!!
Pourquoi le mouvement de la Lune est-il si compliqué ?
Le mouvement d'une planète comme Mercure autour du Soleil est beaucoup plus simple que le mouvement de la Lune autour de la Terre. D'où vient cette différence?
Les forces mises en jeu sont de même nature : ce sont des forces gravitationnelles. Le corps céleste gravite autour d'un axe central (le Soleil pour Mercure, la Terre pour la Lune) et est perturbé par l'influence gravitationnelle des autres astres. Cependant, les ordres de grandeurs de masse de l'astre central et des astres perturbateurs sont différents selon que l'on étudie le mouvement de la Lune ou celui de Mercure.
Lorsqu'on étudie le mouvement de Mercure autour du Soleil, les autres planètes ont une masse très petite par rapport à celle de l'astre central et de plus, les planètes sont très petites par rapport à la distance Mercure-Soleil et par rapport aux distances entre Mercure et les autres planètes : en première approximation, donc, Mercure est un simple point matériel en interaction avec le Soleil, l'influence des autres planètes se traitant comme une petite perturbation de cette approximation.
Le cas de la Lune, soumise à l'attraction du Soleil et de la Terre principalement, est plus compliqué : assimiler la Lune et la Terre à des points matériels, c'est faire une approximation beaucoup plus grossière; de plus, un des astres susceptibles de perturber la trajectoire de la Lune, le Soleil, est beaucoup plus massif que l'astre central. C'est ainsi qu'au XVIIième siècle, alors que l'on souhaitait disposer d'une horloge suffisamment précise pour que la marine puisse mesurer les longitudes avec une précision raisonnable pour éviter les nombreux naufrages qui avaient lieu à cette époque, le mouvement de la Lune, qui avait d'abord été considéré comme une horloge "naturelle" possible, a dû être abandonné au profit d'horloges mécaniques... Aucun des calculs de l'époque n'avait réussi à prédire le mouvement de la Lune avec assez de précision pour que ces prédictions puissent servir dans la marine.
Un coup d'oeil sur les forces s'exerçant sur la Lune
La Lune, en première approximation, est soumise à l'action gravitationnelle du Soleil et à celle de la Terre. Comparons ces deux forces :
la norme de la force FS exercée par le Soleil sur la Lune est :
FS = G MS ML/SL2
et celle de la force FT exercée par la Terre sur la Lune est
FT = G MT ML/TL2
(SL = distance Soleil-Lune ≃ distance Soleil-Terre ≃ 1,5 × 1011 m, TL = distance Terre-Lune ≃ 3,8 × 108 m, MS = masse du Soleil ≃ 1,989 × 1030 kg, MT = masse de la Terre 5,98 × 1024 kg)
Si on fait le rapport entre ces deux forces, FS/FT, on obtient un rapport de 2 environ : les deux forces sont donc du même ordre de grandeur. La trajectoire de la Lune, dans le référentiel de Copernic est effectivement une trajectoire complexe associant un mouvement de rotation autour du Soleil à un mouvement de rotation autour de la Terre.
Le problème devient plus simple si on le considère dans le référentiel géocentrique, comme on le fait généralement en lycée. Effectivement, comme la Terre et la Lune sont quasiment à la même distance du Soleil, elles subissent de la part de ce-dernier quasiment la même accélération. Par suite, en se plaçant dans le référentiel géocentrique, en première approximation l'accélération subie par la Lune de la part du Soleil s'élimine avec l'accélération de la Terre.
Toutefois, et c'est là la source de la complexité du mouvement de la Lune, cette simplification n'est possible qu'en première approximation : l'influence du Soleil sur la Lune est la perturbation majeure que subit la Lune dans le référentiel géocentrique, devant les autres perturbations que constituent les effets de non-sphéricité de la Terre, l'influence des autres planètes, etc...
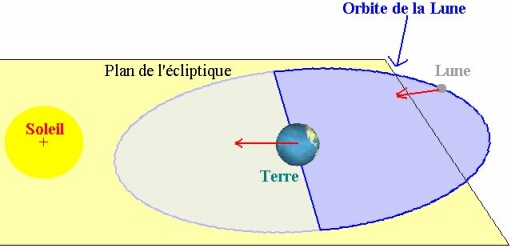
En fait, lorsque la Lune se déplace sur son orbite autour de la Terre, elle est tantôt un peu plus près du Soleil que la Terre, tantôt un peu plus loin qu'elle : quand la Lune est plus près, elle est sur une orbite plus basse, et, par suite, elle subit une accélération, dans le référentiel de Copernic, de norme plus importante que celle de la Terre. Lorsque la Lune est plus loin, elle est sur une orbite plus haute, et elle subit donc une accélération de norme plus faible que celle de la Terre. De plus, les directions de l'accélération subie par la Lune de la part du Soleil et de celle subie par la Terre sont légèrement différentes.
Cette image, qui ne respecte aucune échelle, donne une idée de la situation : la Lune, plus éloignée que la Terre, subit de la part du Soleil une accélération (vecteur en rouge) de norme plus faible que celle de la Terre. La direction de cette accélération, qui est dans les deux cas dirigée vers le Soleil, est différente lorsque la Lune, la Terre et le Soleil ne sont pas complètement alignés, c'est-à-dire en-dehors des éclipses (comme le plan de l'orbite de la Lune fait un angle de 5° environ avec le plan de l'écliptique, ces trois corps célestes ne sont pas généralement alignés en période de nouvelle ou de pleine Lune)
Lorsqu'on soustrait les accélérations pour se placer dans le référentiel géocentrique, on se retrouve donc avec des termes perturbatifs résiduels. L'importance relative de ces termes, due à la masse très importante de l'astre perturbateur (ici le Soleil), fait du calcul de la trajectoire précise de la Lune un problème très délicat, source de nombreuses difficultés.
Conclusion
Etudier la trajectoire de la Lune dans le référentiel géocentrique en considérant que l'on a seulement un système isolé Terre + Lune est tout à fait légitime, mais à condition de savoir que, contrairement aux résultats obtenus avec des astres moins fortement perturbés (comme Mercure, Mars, etc.), les résultats obtenus pour la Lune sont fortement entachés d'erreur... En effet, les grandeurs caractéristiques de la trajectoire de la Lune ne peuvent pas être données avec un grand nombre de chiffres significatifs (généralement 2 ou 3 chiffres seulement) à moins d'être des valeurs moyennes ou les valeurs correspondant à une date précise (auquel cas on peut obtenir une bien meilleure précision).
La Lune, si près de nous, est un astre dont le calcul de la trajectoire précise est longtemps resté un défi...
Pour citer cet article :
Perturbations de la trajectoire de la Lune, Gabrielle Bonnet, septembre 2004. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Lune.xml