Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Introduction à la relativité
26/06/2012
Résumé
Première approche de la relativité restreinte élémentaire et imagée : nouvelle perception du temps et de l’espace, notions de « distance-temps » invariante, de temps propre et d'horizon. Le cas d'une fusée accélérée est abordé.
Table des matières
- 1. Repérage dans l’espace-temps
- 2. Géométrie de l’espace-temps avec c = 1 : unité unique de temps et de longueur
- 3. Masse et énergie
- 4. Transformation de Galilée
- 5. Transformation de Lorentz
- 6. Distances dans l’espace-temps : quadri-repères et causalité
- 7. Dilatation du temps et contraction des longueurs
- 8. Le temps propre et les jumeaux de Langevin
- 9. Trajectoire d’une fusée accélérée
- 10. Effets de l’accélération dans la fusée
- Conclusion
Comment la relativité nous oblige-t-elle à revoir la perception intuitive de temps et d’espace ? Avec un « espace-temps » à quatre dimensions, la coordonnée de temps n’est plus différenciée de celles de l’espace. Quelle conséquence en tirer sur les unités de mesure ? Un observateur étant associé à son propre « quadri-repère » dans l’espace-temps, comment la relativité modifie sa perception des « événements » et limite son espace-temps observable ? Ces différentes questions sont abordées et illustrées pour un lecteur qui n’a pas de connaissance initiale sur la relativité.
Cet article est basé sur un exposé présenté à une classe de lycée en 2005 lors de l’année mondiale de la physique.
Une autre présentation de la relativité dans l’article « Relativité et vitesse de la lumière » (Gabrielle Bonnet 2003) décrit l’apport essentiel d’Einstein, propose des exemples différents et des prolongements.
Une conférence sur la « Relativité restreinte » (Marc Vincent 2012) permet de retracer l'histoire de cette notion, fournit des applications concrétes et des animations sur le sujet.
1. Repérage dans l’espace-temps
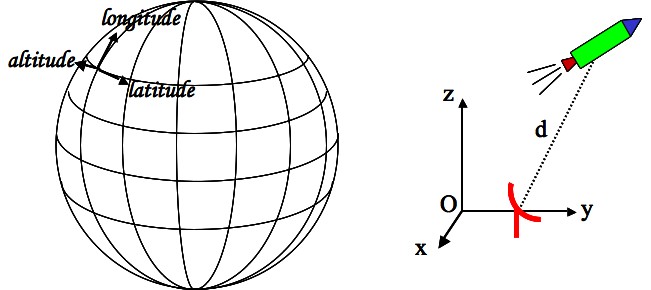
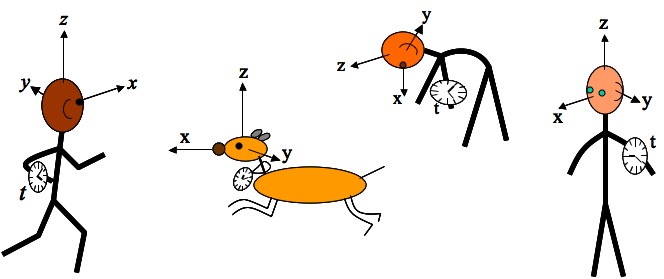
L’espace usuel est à trois dimensions : longueur, largeur et hauteur, ou longitude, latitude et altitude, ou les coordonnées x, y, z dans un repère cartésien.
Les trois coordonnées d’un repère n’ont pas de signification absolue.
Seule la distanced entre deux points a une réalité physique. En fonction de leurs coordonnées cartésiennes x1, y1, z1 et x2, y2, z2le carré de la distance vaut : (théorème de Pythagore généralisé de deux à trois dimensions).
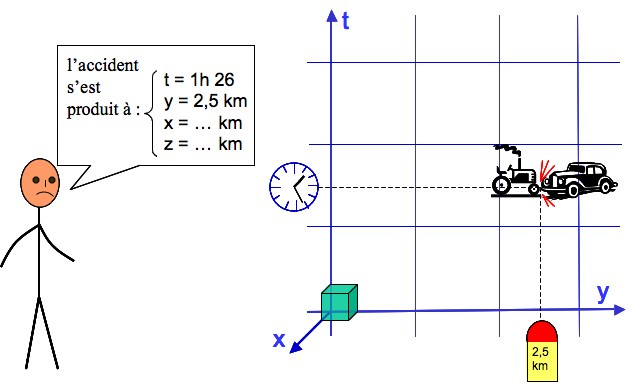
Notre espace-temps est à quatre dimensions. Un événement est un point de l’espace-temps, comme par exemple l’accident schématisé figure 2.
Si un individu A fixe un rendez-vous avec son ami B : « demain à 13h30 », il suppose que B sait de quelle heure il s’agit. C’est généralement l’heure locale du lieu de rendez-vous, qui dépend du fuseau horaire et du pays. Par exemple les horaires d’avions sont donnés en heures locales des lieux de départ et d’arrivée. Les individus A et B peuvent aussi convenir d’utiliser le temps universel (TU ou GMT, heure de Greenwich).
Les deux amis, après avoir synchronisé leurs montres, doivent aussi supposer qu’elles indiqueront exactement la même heure au même instant le lendemain.
Est-ce que le temps est une grandeur universelle ? C’est une question que se posait Einstein et qui l’a conduit à la théorie de la relativité.
Voir aussi l'article « Relativité et vitesse de la lumière ».
La relativité est fondée sur le principe que tout phénomène physique se produit à l’identique dans tous les référentiels galiléens.
On appelle galiléens les référentiels en mouvement de translation uniforme par rapport à un référentiel quelconque de référence que nous dirons fixe ou immobile. Les référentiels en rotation ne sont pas galiléens : une conséquence est la force centrifuge que l’on ressent dans un véhicule qui tourne. La terre tourne par rapport à un référentiel lié au soleil ou aux étoiles. Si l’approximation de référentiel galiléen est possible pour les phénomènes courants à l’échelle humaine, elle n’est plus valable pour les phénomènes à grande échelle tels que vents, marées ou pour des mesures très précises, par exemple celles du GPS.
En particulier, les lois de l’électro-magnétisme sont les mêmes et, par conséquent, les ondes lumineuses se propagent dans le vide à la même vitesse, quel que soit le référentiel. Puisque la vitesse de la lumière dans le vide est invariante, sa grandeur c devient une constante fondamentale universelle sur laquelle est fondée la théorie de la relativité.
2. Géométrie de l’espace-temps avec c = 1 : unité unique de temps et de longueur
La valeur de c, vitesse de la lumière dans le vide, fournit un rapport fixe entre les mesures de temps et de longueur. Si le temps t n’est plus considéré comme une grandeur particulière, mais correspond à la quatrième dimension de l’espace-temps, il devient naturel de mesurer les quatre coordonnées x, y, z et t avec la même unité: le mètre, la seconde, ou leurs unités dérivées. En physique relativiste, la façon la plus simple d’unifier les unités de temps et d’espace est de fixer c = 1, ce qui est systématiquement fait dans la suite.
On peut alors exprimer les distances suivantes en unité de temps :
- la lune est à 1,5 secondes de la Terre.
- la distance terre-soleil est de 8 minutes.
- Pluton est distant du soleil de 5 heures environ.
- l’étoile Sirius est distante de 8,6 années (ce qui équivaut à 8,6 « années-lumière », unité courante en astronomie).
- la longueur d’un « double-décimètre » est de 0,67 ns (0,67.10-9 s).
Inversement, exprimons quelques durées en unité de longueur :
- une seconde vaut environ 300 000 km.
- la durée de rotation de la terre sur elle-même, une journée, vaut 2,6.1010 m.
- le temps de réponse d’un système électronique (environ 1 ns) vaut 30 cm.
La vitesse de la lumière dans le vide étant fixée par c = 1, la vitesse v devient une grandeur sans dimension (v remplace le rapport v/c qui apparaît souvent).
On pourra vérifier les valeurs suivantes :
- la vitesse de rotation de la terre autour du soleil : v ~ 10-6
- la vitesse de rotation de l’électron autour du noyau d’hydrogène : 1/137 (selon le modèle classique de l’atome de Bohr).
- la vitesse typique d’un neutron « rapide » de réacteur nucléaire : v ~ 1/10
Il est intéressant de remarquer que l’unité de longueur est également reliée à l’unité de temps dans le système international d’unités.
En effet, depuis 1983, l’unité internationale de longueur, le mètre, est fixée par rapport à l’unité de temps, la seconde, en fixant désormais la vitesse de la lumière dans le vide à la valeur exacte suivante c = 299 792 548, 000 m.s-1.
Voir le site officiel du BIPM (Bureau International des Poids et Mesures)
Cette nouvelle définition du mètre est liée aux performances des lasers. Ils permettent des mesures de plus en plus précises des fréquences et des longueurs d’onde, donc de la vitesse de la lumière. Avec la définition indépendante de l’unité de longueur adoptée en 1960, on ne pouvait plus améliorer la précision sur la mesure de c.
3. Masse et énergie
En mécanique relativiste, un corps de masse m au repos contient l’énergie E = m : c’est la relation d’Einstein E = mc2, écrite ici avec c = 1.
Les masses et les énergies s’expriment indifféremment en gramme g ou en joule J :
Tableau 1. Exemples de masses et énergies
en gramme (g) | en joule (J) | |
|---|---|---|
la masse du proton | 1,6.10-27 g | 1,5.10-10 J |
un gramme de matière | 1 g | 0,9.1014 J |
l’énergie de 1 tep (combustion d’une tonne de pétrole) | 4,7.10-4 g | 4,2.1010 J |
Les lois de la dynamique lient la norme p de la quantité de mouvement et
l’énergie E d’un corps en mouvement par la relation fondamentale suivante qui est
valable dans chaque référentiel :
La vitesse ainsi que le facteur dépendent du référentiel. L’énergie E est la somme de l’énergie au repos m et de l’énergie cinétique Ec . Dans la limite non-relativiste où p ≪ m, on retrouve .
4. Transformation de Galilée
Pour un observateur immobile dans un référentiel de référence R, un événement de l’espace-temps a lieu au point X = {x, y, z, t}. Un observateur en mouvement à la vitesse v selon l’axe Ox mesure les coordonnées de l’événement dans son référentiel R’, soit X’ = {x’, y’, z’, t’}.
En cinématique usuelle, on déduit X’ de X et t par la transformation simple de Galilée. Seule la coordonnée x est modifiée. Le temps t = t’ est alors universel.
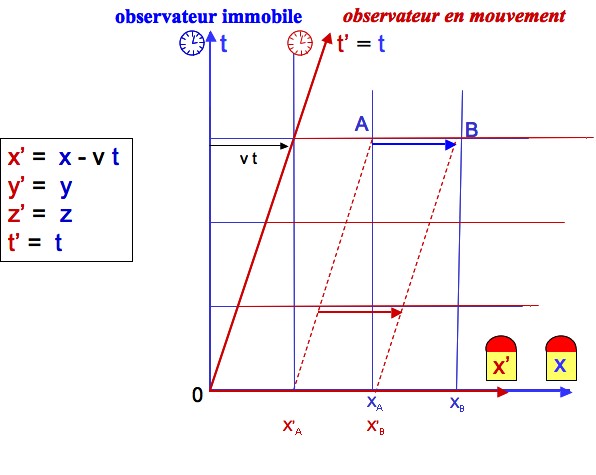
La transformation de Galilée est schématisée par la figure 3.
Pour l’observateur immobile (repère bleu), le référentiel en mouvement apparaît avec l’axe des temps incliné (repère rouge), la pente étant égale à 1/v.
Avec , on voit par exemple que le point A (xA = 2, t = 3) se trouve à (x’A = 1, t’ = 3) dans le repère rouge.
Une propriété importante de la transformation de Galilée est de conserver les distances, comme les durées. On vérifie par exemple que la distance AB est la même pour les référentiels R et R’ : x’B - x’A = xB – xA.
5. Transformation de Lorentz
On considère à nouveau l’observateur en mouvement à la vitesse v dans la direction de l’axe Ox. Si la vitesse v est très "grande", typiquement si elle est supérieure à environ 1/10 (rappelons que c = 1), la transformation de Galilée est une approximation insuffisante. C’est la transformation de Lorentz qui permet de passer du repère R de coordonnées x, y, z et t au repère R’ de coordonnées x’, y’, z’ et t’. Elle mélange la coordonnée de temps t avec la coordonnée d’espace x. L’intervalle de temps entre deux événements n’a plus de valeur absolue, elle dépend de l’observateur.
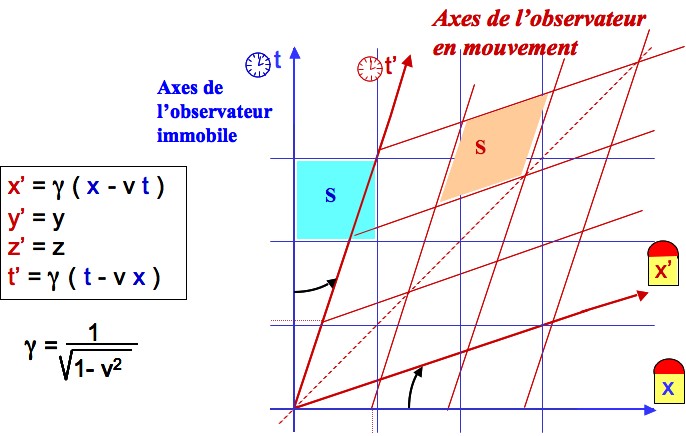
Le schéma de la figure 4 montre comment se déforme le repère R (bleu) quand on change de référentiel. Les axes du repère R’ (rouge) font des angles de tangentes v et 1/v avec ceux du repère R. Une surface telle que S qui est un carré pour l’observateur immobile est un losange pour l’observateur en mouvement.
On peut vérifier que la transformation inverse de R’ en R est exactement de la même forme algébrique avec un signe opposé pour v.
Dans l’approximation non-relativiste : v ≪ 1 et γ ≈ 1 , on retrouve la transformation de Galilée, en remarquant que , car pour un observateur toute distance x est généralement très petite devant le trajet de la lumière pendant la durée t d’observation.
Une propriété importante de la transformation de Lorentz est l’invariance par changement de référentiel de la grandeur suivante :
C’est analogue à la propriété d’invariance (carré de la distance) par rotation du repère dans l’espace usuel.
La transformation de Lorentz s’applique également au quadri-vecteur dont les quatre coordonnées sont les trois composantes de la quantité de mouvement et l’énergie totale :
L’invariant dans cette transformation est le carré de la masse
Si la particule est au repos dans le repère R’, v est sa vitesse dans R et l’on a
et .
Le rapport est le facteur de Lorentz de la particule. Ce dernier augmente avec la vitesse v et tend vers l’infini dans le cas ultra-relativiste quand v s’approche de la limite 1.
6. Distances dans l’espace-temps : quadri-repères et causalité
La mesure d’une quadri-distance de l’espace-temps est invariante par changement de référentiel et indépendante du quadri-repère.
Entre deux événements notés A et B, la quadri-distance D est donnée par
La propriété essentielle de D est d’être indépendante du référentiel.
Soit d la distance géométrique et T l’intervalle de temps entre les deux événements, mesurés dans un même référentiel.
La relation conduit à trois situations physiques différentes, selon que d > |T| , d < |T| ou d = |T| .
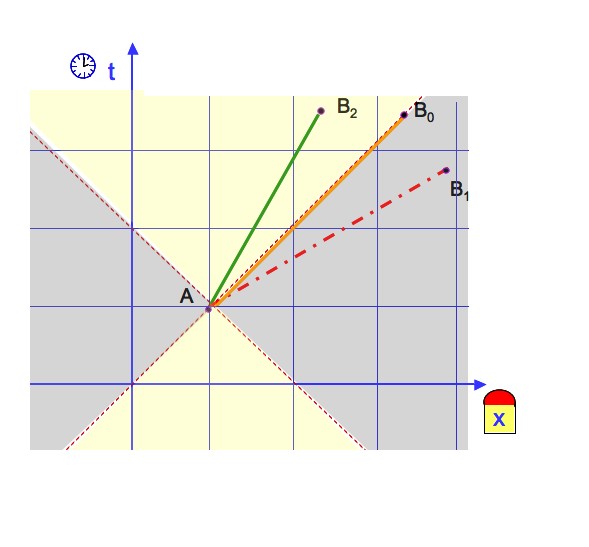
La figure 6 schématise pour chaque cas les trajets entre le point A et un autre point B du plan Oxt. La bissectrice (pointillés rouge) correspond au trajet AB effectué à la vitesse de la lumière v = 1.
Le premier cas d > |T| est représenté par le trajet AB1. Sa pente dx/dt par rapoort à l'axe du temps est une vitesse supérieure à celle de la lumière. Aucun objet ni signal ne peut effectuer un tel trajet, ni le trajet inverse. Les points A et B1 sont non-causaux entre eux.
Le point A ne peut ni voir, ni être influencé par les événements situés dans la portion d’espace indiquée en gris.
Le deuxième cas d < |T| est représenté par le trajet AB2. Sa pente correspond à un trajet possible effectué de A vers B2 à une vitesse inférieure à celle de la lumière. La durée du trajet entre A et B2, vécue par le voyageur, est égale à , le nombre D étant imaginaire. On appelle τ le temps propre du trajet.
Le trajet inverse de B2 en A est impossible, car le temps doit être croissant : l’événement A est dans le passé de B2 et l’événement B2 dans le futur de A.
Le troisième cas d = |T| est un cas limite représenté par le trajet de A vers B0. Il correspond à une propagation à la vitesse de la lumière v = 1. L’onde lumineuse effectue le trajet de A vers B0 avec D = τ = 0. Son temps propre est nul.
7. Dilatation du temps et contraction des longueurs
Une conséquence du facteur γ qui apparaît dans la transformation de Lorentz est l’effet relativiste de dilatation du temps et celui, inverse, de contraction des longueurs.
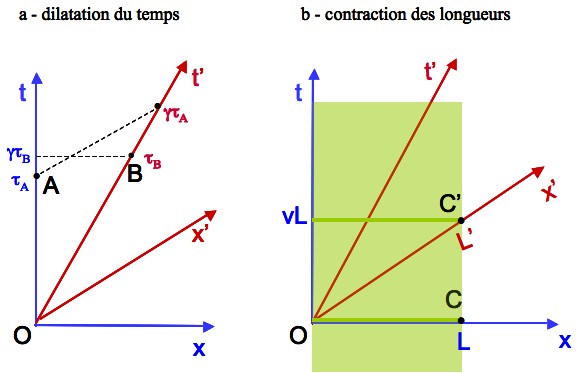
Soient deux observateurs QA et QB, le second étant en mouvement par rapport au premier avec une vitesse v selon Ox. Leurs référentiels sont notés R et R’. On considère un segment OA de la trajectoire de QA dans l’espace-temps (figure 7a). Dans le référentiel R de QA, les coordonnées (x,t) du début et de la fin de ce segment sont (0, 0) et (0, τA). D’après les formules de Lorentz, elles sont (x’, t’) = (0, 0) et (-γvτA, γτA) dans le référentiel R’ de QB. Pour l’observateur QB le parcours OA de QA a donc une durée γτA, supérieure à celle que QA a expérimentée. C’est ce qu’on nomme la dilatation du temps.
Les temps τA et τB sont les durées propres des parcours OA et OB. La durée propre est la durée minimum d’un parcours quand on fait varier le référentiel. Elle est obtenue dans le référentiel où le parcours se fait à vitesse nulle.
La dilatation des temps est bien vérifiée avec les particules élémentaires instables telles que le muon. En leur communiquant une grande énergie on augmente par le facteur leur durée de vie moyenne dans le laboratoire.
Voir l'animation sur l'expérience des muons dans l'atmosphère
Considérons maintenant une barre solide de longueur L, immobile dans R et occupant le segment OC à t = 0. Cet objet balaye une surface dans l’espace-temps, la bande verticale verte sur la figure 7b. La barre est vue dans R’ comme un objet en mouvement occupant le segment OC’ à t’ = 0. Les coordonnées de C’ sont (x, t) = (L, vL) dans R et (x’, t’) = (L’, 0) dans R’. Appliquant la transformation de Lorentz inverse qui donne x = γ(x’+vt’), on obtient L’= L/γ.
On peut aussi obtenir ce résultat en écrivant que L’ est la quadri-distance invariante OC’, donnée dans R par L’2 = x2(C’) - t2(C’) = L2- v2L2 = L2/γ2.
La longueur L’= L/γ est donc inférieure à la longueur L. C’est la contraction des longueurs. Elle n’affecte que la coordonnée longitudinale, les dimensions transverses étant respectées. La longueur de la barre est maximum dans le référentiel où elle est immobile.
Malgré ce qui précède, si on regarde un objet en mouvement relativiste, il n’apparaît pas aplati, mais de proportions normales. Par contre il apparaît tourné par rapport à la direction du mouvement. Ceci vient du fait que les signaux lumineux émis par les différentes parties de l’objet mettent des temps différents pour nous parvenir. On n’a pas une photo « à t = constante ».
On trouve les mêmes effets de dilatation du temps et de contraction des longueurs, avec le même facteur γ que l’on passe de R à R’ ou de R’ à R. Il suffit de considérer que l’observateur du référentiel R est en mouvement relatif de vitesse – v par rapport au référentiel R’. Sur les figures 4 et 7, on a choisi de représenter un des repères, celui du référentiel R, par des axes orthogonaux Oxt (en bleu). Un choix différent est possible.
8. Le temps propre et les jumeaux de Langevin
La dilatation du temps d’un référentiel en mouvement est couramment invoquée pour établir le résultat paradoxal des « jumeaux de Langevin ». L’un reste sur terre, tandis que l’autre voyage au loin à grande vitesse et revient après de nombreuses années. Au retour, chacun constate que le jumeau voyageur est moins vieilli que le jumeau sédentaire, car le temps propre vécu par le jumeau voyageur est inférieur au temps du référentiel terrestre où ils se retrouvent.
Le paradoxe est que l’on arriverait au résultat inverse en considérant que c’est le jumeau sédentaire qui est en mouvement relatif par rapport au jumeau voyageur. Il y a donc une dissymétrie entre le référentiel terrestre et le référentiel du jumeau voyageur.
La démonstration suivante est basée sur l’invariance de la quadri-distance dans l’espace-temps. On en déduit une inégalité triangulaire sur les temps propres inverse de celle des distances usuelles.
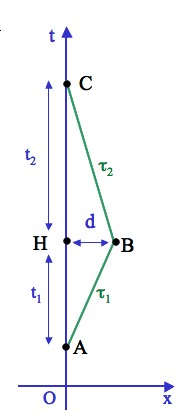
Figure 8. Les trajets des jumeaux dans l’espace-temps
La figure 8 représente les axes de l’espace-temps du référentiel R du jumeau sédentaire et les points des trois événements suivants : A, le départ du jumeau voyageur, B l’événement du demi-tour que nous supposons instantané, C la rencontre au retour. On suppose qu’il a effectué chacun des trajets à vitesse constante, v1 à l’aller AB et v2 au retour BC. On note τ1 et τ2les temps propres de ces trajets et d la distance d’éloignement HB avant son demi-tour.
Calculant les temps propre dans le référentiel R (voir le deuxième cas dans la partie 6) on a et .
On en déduit et soit
Donc le temps propre total du jumeau voyageur est inférieur à celui du jumeau sédentaire. Il n'est pas nécessaire de passer par la relativité générale pour établir ce résultat.
La dissymétrie entre les deux jumeaux provient du fait que le référentiel du jumeau voyageur a changé au point de demi-tour.
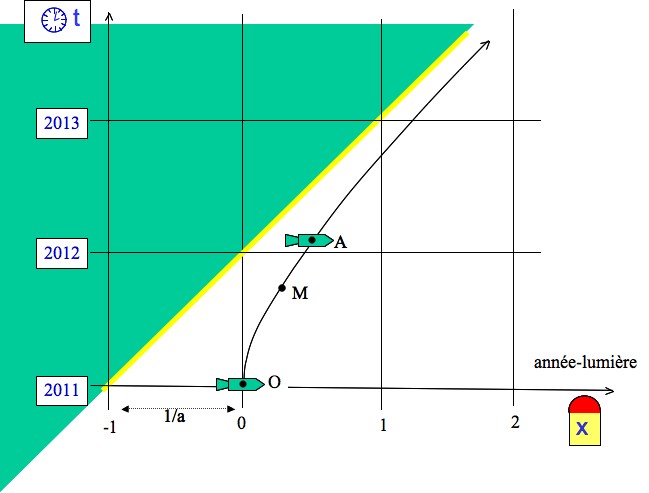
9. Trajectoire d’une fusée accélérée
On considère une fusée accélérée. A chaque point M du voyage, on associe le référentiel instantané de la fusée Rf(M). On a donc une suite infinie continue de référentiels galiléens. On suppose que l’accélération au point M, mesurée dans le référentiel Rf(M), est une constante a.
L’accélération d2x / dt2 dans le référentiel R n’est pas constante. L’accélération dans le référentiel Rf vaut a = F/m, rapport entre la force F de propulsion et la masse m de la fusée. Elle est constante si la force F est continuellement ajustée afin de compenser la diminution de la masse m due à la consommation de carburant. On peut montrer que la force selon Ox est identique dans les référentiels R et Rf.
Figure 9. Trajectoire d’une fusée accélérée dans l’espace-temps
L’équation de l’hyperbole est
Pour établir cette équation, on écrit les expressions donnant la force en fonction des dérivées de la quantité de mouvement p et de l’énergie E, soit et .
On obtient par intégration et .
La relation conduit à
La fusée part de l’origine t = x = 0 avec la quantité de mouvement p = 0 et l’énergie E = m, on a donc t1 = 0 et x1 = -1/a
Le temps propre τ de la fusée est lié au temps t par , le facteur relativiste γ dépendant du temps.
En intégrant on obtient la relation . On fait apparaître le temps propre τ dans l’équation paramétrique de l’hyperbole :
Dans cet exemple, avec a = 1 an-1 = 9,50 m.s-2, on considère le point A que la fusée atteint après un temps propre τ = 1 an. Dans le référentiel R, on mesure alors une vitesse v = 0,7616 c, le temps est alors t = 1,175 an et la distance parcourue x = 0,543 année-lumière.
Quand la vitesse de la fusée s’approche de la vitesse de la lumière, l’hyperbole tend vers son asymptote d’équation x = t - 1/a (soulignée en jaune), qui représente un horizon pour la fusée. En introduisant les coordonnées y et z, c’est un hyper-plan à trois dimensions dans l’espace-temps. Aucun signal lumineux émis derrière l’horizon (zone en vert) ne peut parvenir à la fusée si celle-ci ne cesse pas d’accélérer.
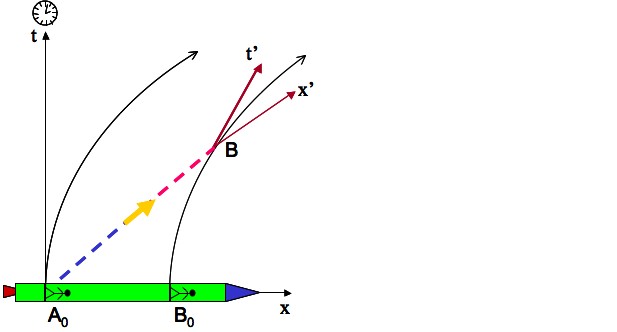
10. Effets de l’accélération dans la fusée
Les deux cosmonautes qui sont à l’intérieur de la fusée ressentent la pesanteur artificielle créée par l’accélération. L’un est en « bas » et l’autre est en « haut », aux points en A0 et B0 à l’instant t = 0. Si le premier envoie en A0 un signal lumineux vers le deuxième, celui-ci le reçoit en B, avec un décalage spectral vers le ‘‘rouge’’ (figure 9).
Ce décalage s’explique par un effet Doppler, dû à l’accroissement ∆V = a.∆h de la vitesse de la fusée entre l’émission en A0 et la réception au point B de l'espace-temps, la distance dans la fusée entre les cosmonautes étant ∆h.
Le décalage relatif de la période T (ou son opposé en fréquence υ) est au premier ordre en ∆h :
Un décalage inverse - a.∆h vers le bleu apparaît pour un signal envoyé du haut vers le bas. Supposons que chacun des cosmonautes dispose d’une horloge atomique ou d’une montre à quartz (insensibles aux effets d’accélération, contrairement à une pendule). Ils comparent leurs mesures δA et δB de l’intervalle de temps entre deux éclairs lumineux se propageant entre A et B. Ils obtiennent comme précédemment le décalage relatif . Ils en déduisent donc que leurs horloges ne tournent pas à la même vitesse, celle d’en bas tournant plus lentement.
En raison du principe d’équivalence, on attend le même effet dans un champ de pesanteur. C’est alors un phénomène qui relève de la Relativité Générale.
Une première confirmation du décalage spectral gravitationnel fut obtenue par Pound et Rebka en 1960. Du haut en bas d’une tour de 22,5 m, ils ont détecté des écarts relatifs de l’ordre de 10-15 sur la fréquence d’une raie gamma du fer radioactif (57Fe, 14 keV).
Le GPS (Global Positionning System) prend également en compte une faible variation de vitesse des horloges en fonction de leur altitude, de l’ordre 10-13 par km. Pour en savoir plus, voir une conférence sur le fonctionnement du Global Positionning System (GPS).
Le GPS utilise un temps "universel", valable à l’échelle de notre planète. Les horloges locales peuvent retarder ou avancer, mais on peut calculer exactement les corrections à faire par rapport au temps universel.
Conclusion
On a résumé quelques résultats essentiels de la relativité restreinte introduite par Einstein. La vitesse c de la lumière jouant un rôle essentiel, on a constamment fixé c = 1 ce qui identifie les unités de temps et de longueur, ainsi que les unités de masse et d’énergie. On a utilisé la représentation géométrique de l’espace-temps et l’invariance de la quadri-distance pour comparer les observations faites à partir de deux référentiels galiléens en mouvement l’un par rapport à l’autre. On montre également quelques résultats de la relativité restreinte concernant le cas d’une fusée accélérée, applicables, grâce au principe d’équivalence, au décalage spectral gravitationnel.
Voir aussi :
- la conférence sur la « Relativité restreinte » (Marc Vincent 2012) qui permet de retracer l'histoire de cette notion, fournit des applications concrétes et des animations sur le sujet.
- l’article « Relativité et vitesse de la lumière » (Gabrielle Bonnet 2003) qui décrit l’apport essentiel d’Einstein, propose des exemples différents et des prolongements.
Pour citer cet article :
Introduction à la relativité, Marie-Christine Artru, Xavier Artru, juin 2012. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Introduction-relativite.xml