Activer le mode zen
Ressource au format PDF
Classification
Le GPS - La physique du GPS (2/2)
15/10/2019
Résumé
Article tiré de la conférence sur le GPS donnée par Jean-Pierre Lièvre à l'ENS de Lyon.
Table des matières
Cet article fait suite au premier volet : Le GPS - Principe de localisation dans l'espace (1/2).
1. Un peu de mécanique : le mouvement des satellites
1.1 Rappel des lois de Kepler
Johannes Kepler (1571-1630) a étudié les mouvements des planètes autour du soleil. Il en a déduit 3 lois qui concernent les problèmes à deux corps qui interagissent uniquement par gravitation, à symétrie sphérique.
Dans le cas du système GPS, on s'intéresse au mouvement d'un satellite autour de la Terre. On se trouve donc dans une situation où un des deux objets a une masse très grande devant l'autre.
On va alors considérer fixe l'objet possédant une très grande masse dans le référentiel galiléen choisi : la Terre, et étudier le mouvement de l'autre objet : le satellite, figure 2.
Les lois de Kepler nous permettent de savoir que :
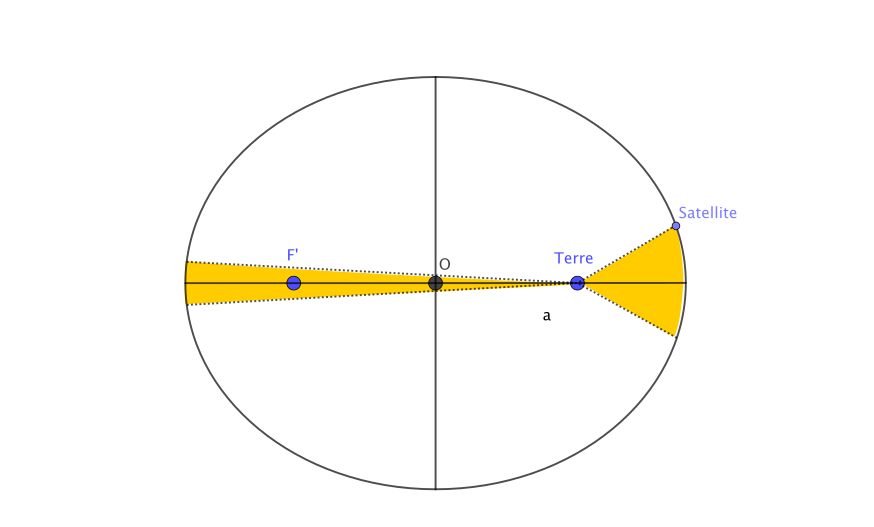
- le satellite décrit une trajectoire elliptique dont un foyer est au centre de force ;
- le mouvement du satellite suit la loi des aires ;
- Le carré de la période du satellite est proportionnelle au cube du demi-grand axe : T2/a3 = cte
1.2 Mécanique de Newton
Figure 3. Reproduction photographique d'un portrait de Isaac Newton (1642-1727) Source : wikimedia |
Nous venons de donner une description cinématique du mouvement des satellites. On peut aussi déduire les résultats de Kepler à partir de deux lois formulées par Isaac Newton, figure 3.
Le principe fondamental de la dynamique indique que le produit de la masse, ici la masse du satellite, par son accélération est égal à la force :
Et, à l'aide de la loi de la gravitation, en supposant que les astres sont à symétrie sphérique, on peut les ramener à des points en leur centre de gravité. On peut formuler la force d'interaction au premier ordre comme :
1.3 Les six éléments de l'orbite
D'après la modélisation précédente, les trajectoires des satellites décrivent des ellipses.
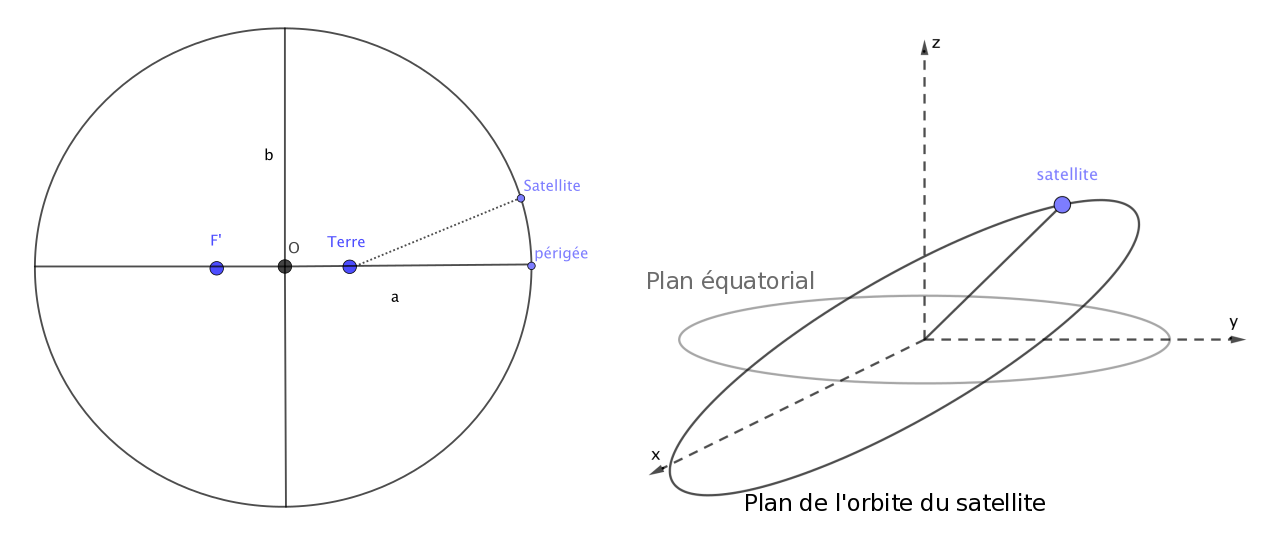
Pour décrire la trajectoire du satellite, il est nécessaire de connaître les paramètres de l'ellipse qu'il suit. Ensuite, il faut repérer ce plan dans le repère terrestre (à l'aide de 4 paramètres) en se basant, par exemple, sur le plan équatorial.
À l'aide de tous ces éléments, il est possible de connaître la loi horaire du mouvement du satellite. En connaisant la date de passage au périgée, on pourra ainsi retrouver exactement la position du satellite.
1.4 Au-delà du problème des deux corps !
Il reste quelques perturbations par rapport au modèle que nous venons d'établir :
- Dans le système GPS, on se trouve au-delà du problème à deux corps. Heureusement, la Terre est quand même un élément dominant.
- La Terre n'est pas non plus vraiment sphérique mais s'en rapproche beaucoup.
- Le référentiel géocentrique n'est pas exactement galiléen car il reste le champ gravitationnel de la lune et du soleil dont il faut tenir compte.
- Et nous n'avons pas tenu compte de la pression de radiation (dûe au rayonnement électromagnétique du soleil).
Les conséquences sont les suivantes :
- Les six éléments de l'orbite évoluent au cours du temps et doivent être réactualisés notamment par des stations de contrôle au sol.
- Il est nécessaire de pouvoir déterminer leur évolution entre deux réactualisations.
2. Un peu de relativité
2.1 Synchronisation des horloges
On s'intéresse maintenant à la synchronisation des horloges.
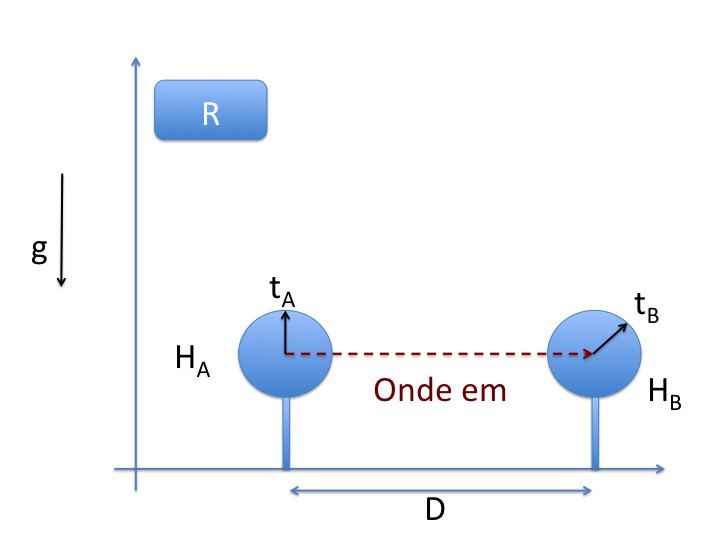
La situation serait simple si les horloges étaient au repos et à la même altitude dans un plan horizontal, figure 5.
L'horloge HB est synchronisée avec l'horloge HA si :
tB = tA + D/c
Cela suppose que la vitesse de propagation des ondes, c, est bien connue et ne dépend ni des points ni des directions choisis.
Mais dans un système GPS, ce n'est pas si simple, car :
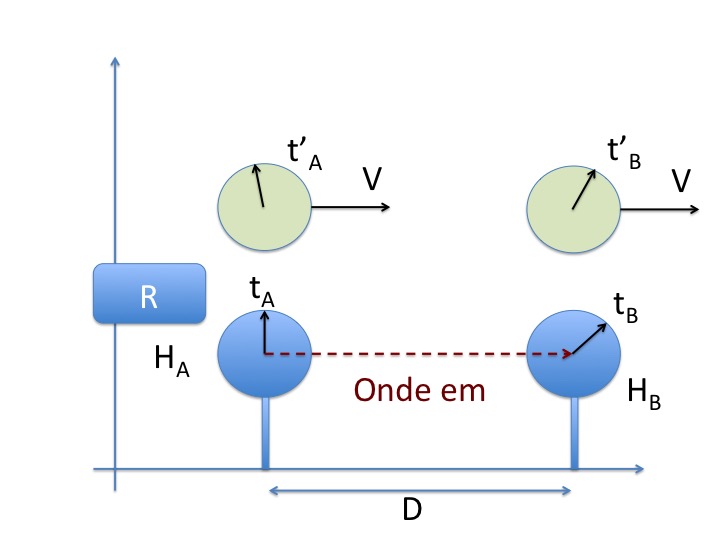
- D'une part, Les horloges sont en mouvement les unes par rapport aux autres, figure 6.
En considérant un satellite se déplaçant à la vitesse V dans le repère R, on mesure maintenant t'A et t'B.
Est-ce que l'on a tB - tA = t'B - t'A ?
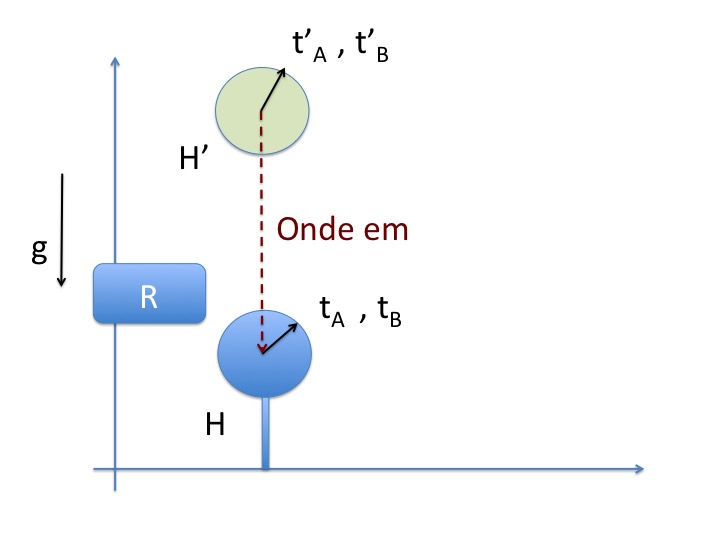
- D'autre part, les satellites ne sont pas sur Terre, mais à une certaine altitude, figure 7.
Est-ce qu'en rajoutant cette donnée, on a encore tB - tA = t'B - t'A ?
C'est ce que nous allons voir maintenant, en nous appuyant sur la théorie de la relativité.
2.2 Synchronisation des horloges et relativité restreinte
En 1905, Albert Einstein propose la théorie de la relativité restreinte qui repose sur les deux postulats suivants :
- Le principe de relativité restreinte : la description des phénomènes est équivalente dans différents référentiels galiléens aussi bien pour la mécanique que pour l'électromagnétisme.
- Le principe d'invariance de la vitesse de la lumière, quel que soit le référentiel galiléen considéré.
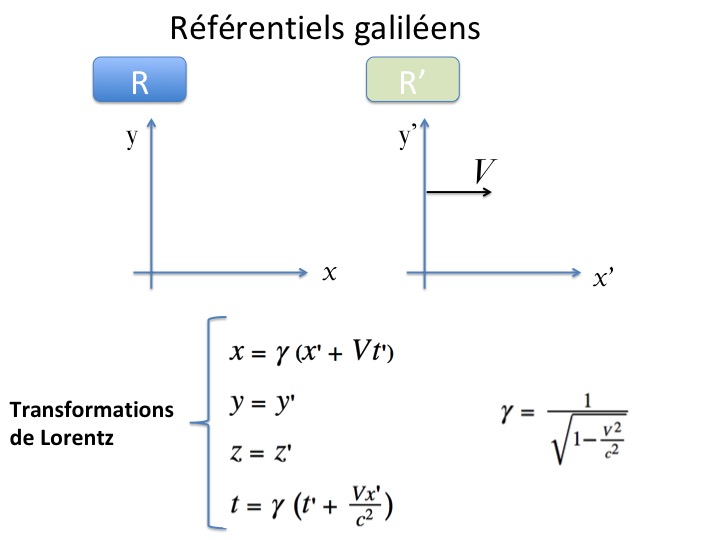
Aujourd'hui avec les transformations de Lorentz, figure 8, il est possible d'établir les équations de propagation d'une onde électromagnétique sans avoir recours au principe d'invariance de la vitesse de la lumière.
L'un des résultats fondamentaux dans la théorie proposée par Einstein c'est que l'espace et le temps se fondent en un « espace-temps ».
Le temps t dans R et le temps t' dans R' ne sont pas les mêmes.
Cela va avoir une conséquence immédiate, figure 9
Horloge mobile : Δt' = t'B - t'A Horloge « fixe » : Δt = tB - tA Δt = γ Δt' › Δt' « Le temps passe moins vite pour les horloges mobiles ! » |
L'intervalle de temps Δt mesuré sur une horloge fixe est supérieur à l'intervalle de temps Δt' mesuré sur une horloge mobile. On observe sur Terre une dilatation des durées. Ainsi, on peut dire, en fonction des horloges : « à chacun son temps... »
Intéressons-nous à ces conséquences dans le système GPS :
Le premier terme de l'équation correspond à la physique classique, le deuxième terme prend en compte les effets relativistes.
Avec une vitesse des satellites utilisés pour le GPS de V = 3,9.103 m/s et pour la vitesse de la lumière, c = 3.108 m/s, au bout d'une journée, on a une erreur de 7 microsecondes, ce qui correspondrait à une erreur de distance cΔt de 2,2 km !
Or, on a besoin d'une précision de quelques dizaines de nanosecondes pour localiser une position au mètre près, on voit ici que l'erreur est beaucoup trop importante !
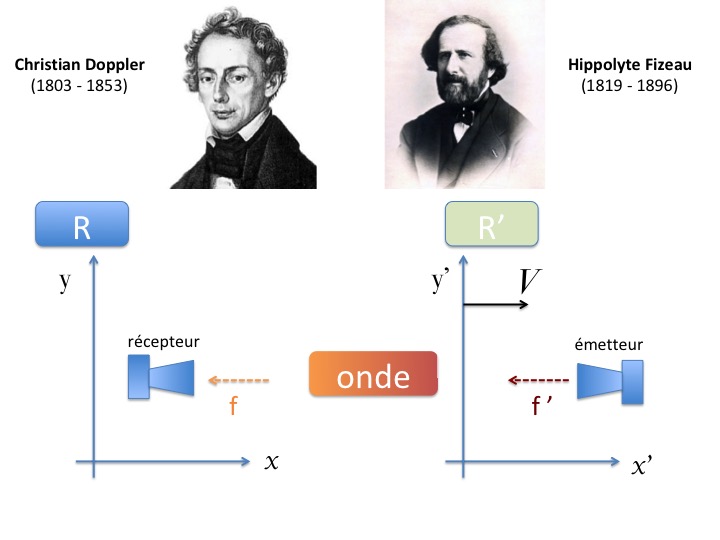
2.3 Interlude sur l'effet Doppler-Fizeau
Soit un émetteur fixe dans un repère R' (par exemple une voiture) et un récepteur fixe dans un autre repère R. L'emetteur se déplace à une vitesse V par rapport au récepteur, figure 10.
Figure 10. Effet Doppler-Fizeau |
On mesure la fréquence d'émission f' dans le référentiel de l'émetteur R' et on mesure la fréquence f reçue par le récepteur dans le référentiel R.
Depuis les travaux de Doppler et Fizeau, on sait que ces deux fréquences sont différentes.
Lorsque l'emetteur s'éloigne, la fréquence f reçue baisse et lorsqu'il se rapproche, la fréquence augmente.
Ces travaux ont été repris pour les ondes électromagnétiques avec une petite correction due à la relativité. Les formules ont été établies par Einstein :
Cette expression correspond au cas le plus simple où le vecteur vitesse V est dirigé dans la même direction que la direction de propagation des ondes.
On aura besoin de la formule approchée de la cinématique classique dans la mesure ou V est très petit devant c. La formule se simplifie en :
Maintenant, du fait de la différence d'altitude entre les horloges embarquées dans les satellites et les horloges terrestres, il faut faire un peu de relativité générale.
2.4 Synchronisation et relativité générale
Galilée (1564-1642) a montré que deux objets différents, par exemple une balle de tennis et une boule de pétanque, jetés du haut d'une tour, arrivent au sol en même temps, s'il n'y a pas de frottements. Elles ont la même loi de chute dans le vide.
Alors, comment interpréter ce phénomène dans la mécanique de Newton ?
Rappelons le principe fondamental de la dynamique :
Où mi est la masse inertielle du corps et mg, la masse gravitationnelle.
L'inertie d'un corps représente le fait qu'un objet inanimé reste dans un état de repos ou en mouvement uniforme. Si l'on veut changer son état de mouvement, l'objet résiste avec une grandeur qui représente son inertie et qui est égale au produit de la masse inertielle par l'accélération imposée.
De l'autre côté de l'égalité, la grandeur F peut s'écrire comme le produit de la masse gravitationnelle par le champ de gravitation.
Ce qui est remarquable dans le cas de la gravitation, c'est que la masse inertielle est la même que la masse gravitationnelle.
Si on écrivait le principe fondamental de la dynamique pour les forces électriques, on aurait toujours le terme de masse inertielle, mais de l'autre côté de l'égalité, se trouverait une grandeur qui caractérise l'objet électrique : sa charge, multipliée par un champ électrique.
Dans le cas de la gravitation, si mi = mg, alors a = g et tous les corps ont la même loi de chute.
Cette égalité avait déjà intrigué Newton qui se demandait s'il ne pouvait pas vérifier expérimentalement cette relation. Comme il n'était pas capable d'étudier de manière précise la chute des corps avec les horloges de l'époque, il a choisi de ralentir le mouvement en constituant des pendules.
En plaçant différents objets au bout de pendules de longueur L, il a pu s'assurer que le rapport masse inertielle à masse gravitationnelle est indépendant de la nature de l'objet.
Ces expériences ont ensuite été reproduites de nombreuses fois.
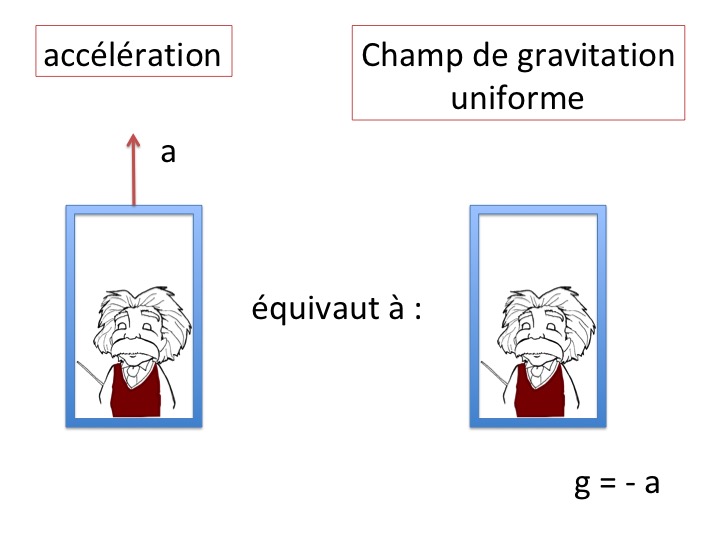
Pour Einstein, cette égalité entre masse inertielle et gravitationnelle un peu fortuite était plutôt fondamentale. Galilée en avait déduit que « le mouvement uniforme était comme rien », et pouvait être interprété simplement par un changement de référentiel. L'interprétation d'Einstein a été différente : « le mouvement accéléré est comme un champ de gravitation ». C'est le principe d'équivalence qu'il établit en 1916.
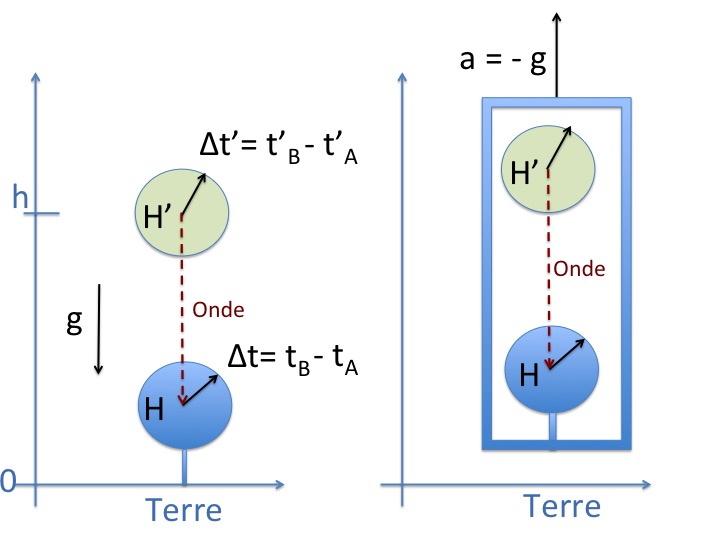
Imaginons quelqu'un dans un ascenseur tenu par un câble. Cette personne est en mouvement accéléré avec une accélération a dirigée vers le haut. Pour cette personne, faisant des expériences de mécanique à l'intérieur, c'est équivalent à l'existence d'un champ de gravitation uniforme g = - a, figure 11.
Ce petit exemple va nous permettre de comprendre pourquoi, lorsque les horloges sont en mouvement, il y a un ralentissement gravitationnel.
Nous avons vu l'effet de la vitesse sur la mesure du temps, intéressons-nous maintenant à l'effet de la gravitation.
Soit une horloge fixe H sur Terre, et une autre horloge H' à l'altitude h. On compare les intervalles de temps Δt' et Δt entre les deux horloges, grâce à une onde électromagnétique.
D'après la théorie de la relativité générale, on peut faire abstraction du champ de gravitation, si l'on imagine que, par rapport au repère lié à la Terre, les deux horloges sont placées dans un ascenseur qui accélère vers le haut, avec une accélération dont la norme égale g, figure 12.
L'horloge H' va émettre une onde électromagnétique, à une période T', pendant une durée lue sur l'horloge Δt'. L'horloge H va recevoir les N crêtes du signal, et mesure l'intervalle de temps lié à la réception.
A priori la période de l'onde reçue n'est pas la même, donc on la note T.
On imagine que l'ascenseur était au repos au moment où le signal part de l'horloge H'. Ainsi le temps que met le signal pour aller de H' à H est environ h/c. La vitesse atteinte est l'accélération multipliée par l'intervalle de temps :
Le récepteur est en mouvement par rapport à l'émetteur. On observe donc une variation de fréquence, c'est l'effet Doppler.
On trouve finalement le lien entre Δt et Δt'.
On en déduit de manière imagée que « le temps passe plus vite en altitude ».
2.5 Application au GPS
L'application au système GPS fait apparaître une petite complication technique : le champ de pesanteur n'est pas exactement uniforme.
Il faut utiliser la loi de variation du champ de pesanteur selon l'altitude z :
Cela amène la comparaison avec les deux intervalles de temps à la formulation suivante :
En combinant les deux effets : la dilatation des durées et l'effet lié aux variations du champ gravitationnel, on trouve la formulation suivante :
L'application numérique donne pour g0 = 9,8 ms-2, RT = 6 400 km, h = 20 200 km, en un jour un écart de 38 microsecondes.
Cet écart se répercute sur la localisation avec une erreur d'environ 12 km !
C'est énorme !
Comment s'y prend-on alors ?
Il faut compenser cette erreur en recalant les horloges à bord des satellites, au moins une fois par jour, en se basant sur les horloges de référence à Terre.
pour approfondir le sujet, on pourra consulter :
- les 3 articles sur « La relativté restreinte » de Marc Vincent.
- l'article « Relativité et vitesse de la lumière » de Gabrielle Bonnet.
3. Un peu d'électromagnétisme
3.1 Propagation dans l'ionosphère
Dans le système GPS, les distances ne vont pas être directement calculées à l'aide de la relation c (tRéception - tEmission), avec c la vitesse des ondes dans le vide.
Les satellites sont à des altitudes très élevées (environ 20 000 km), donc l'essentiel du trajet a lieu dans le vide. Mais en se rapprochant de la Terre, l'onde va entrer notamment dans l'ionosphère comprise entre 50 km < z < 1 000 km.
L'ionosphère est :
- un milieu ionisé qui interagit avec le rayonnement solaire ;
- un milieu variable dans le temps : on observe des variations importantes dans le temps des densités électroniques Ne(z,t) créées par l'interaction avec le soleil. Ces variations dépendent de l'altitude et du moment (alternance jour/nuit, saisons, activité solaire) ;
un milieu dispersif. Dans le vide, la vitesse de phase est indépendante de la pulsation, et vφ = c. Dans l'ionosphère, il existe une interaction entre l'onde électromagnétique et les électrons présents, la vitesse de phase des ondes est alors fonction de leur fréquence ou de leur pulsation vφ(ω).
Lorsqu'on module le signal pour transmettre l'information aux récepteurs sur Terre, les modulations vont se propager à une vitesse qui n'est pas la vitesse de phase, mais la vitesse de groupe : vg(ω).
Une petite modélisation simple de la propagation dans le plasma ionosphérique serait la suivante :
Où ωp dépend de la densité d'électrons Ne(z,t), figure 13.
Il est possible d'avoir accès à la carte de répartition de densité électronique (TEC : intégration de la densité électronique en altitude) de l'ionosphère. On pourra, par exemple consulter la carte de l'ionospèhre en temps réel, sur le site de la NASA.
Classiquement on définit aussi un indice de réfraction ng, comme le rapport de la vitesse de l'onde par la vitesse de groupe :
On trouve un indice dépendant du carré de la fréquence et de la densité d'électrons.
On appelle Δt le retad de propagation dans l'ionosphère. Lorsqu'on le multiplie par c, on trouve l'écart de distance parcouru. On intègre sur toute l'ionosphère par paliers de distance ds :
D' est la distance que l'on cherche.
On remarque qu'il est nécessaire de connaître la densité d'électrons Ne sur l'épaisseur de l'ionosphère.
Il existe plusieurs technologies de récepteurs GPS : des appareils monofréquences et des bifréquences. Le système bifréquence va permettre de réaliser deux mesures de la distance D' aux fréquences f1 et f2.
et avec
À l'aide de ces deux mesures, on élimine le terme dépendant de l'évolution de la densité de charge pour accéder directement à la distance D'.
Pour les appareils fonctionnant en monofréquence, il reste nécessaire de modéliser l'ionosphère pour connaître le profil de la densité électronique et sa variabilité au cours du temps, figure 14.
Il est possible d'avoir accès à la répartition et contenance électronique (TEC) de l'ionosphère. On pourra, par exemple consulter la carte de correction du retard dans l'ionospèhre, sur le site du Global Differential GPS system.
3.2 À l'approche de la Terre
Lorsqu'on se rapproche de la Terre, dans les cinquante premiers kilomètres, on a une nouvelle perturbation liée aux premières couches de l'atmosphère. Le milieu est composé de diazote (N2), dioxygène (O2), Argon (Ar), dioxyde de carbone (CO2) et de vapeur d'eau (H2O).
Aux fréquences auxquelles fonctionnent le GPS (f < 15GHz), le milieu est non dispersif. On ne peut donc pas faire de compensation bifréquence.
Le retard dû à la propagation est de la même forme que celui dans l'ionosphère :
De la même manière que pour l'ionosphère, on modélise l'indice du milieu, mais cette fois en séparant les contributions liées aux différents gaz et de l'autre côté les contributions liées à la vapeur d'eau.
La modélisation de l'indice correspondant à l'air sec est relativement simple et peut s'écrire comme une loi de proportionalité avec la masse volumique des différents gaz.
Pour la vapeur d'eau, la formulation est un peu plus compliquée et pose un véritable problème car la concentration dépend des conditions météorologiques locales : présence de nuages et variabilité rapide du temps. Pour une précision optimale, il est donc nécessaire de connaitre la localisation et la concentration de vapeur d'eau en temps réel et cela, sur toute la surface de la Terre.
Actuellement c'est le terme qui dépend de la modélisation de la vapeur d'eau dans l'atmosphère qui est le plus limitatif pour la précision du GPS.
On imagine des systèmes capable de coupler les récepteurs avec des LIDAR de manière à viser dans la direction du satellite pour connaître localement la contribution liée à la vapeur d'eau en fonction de l'altitude.
La physique du GPS est très riche !
Regardons maintenant comment ces systèmes sont organisés au niveau technique.
4. Pratique du positionnement global
4.1 Les 3 segments
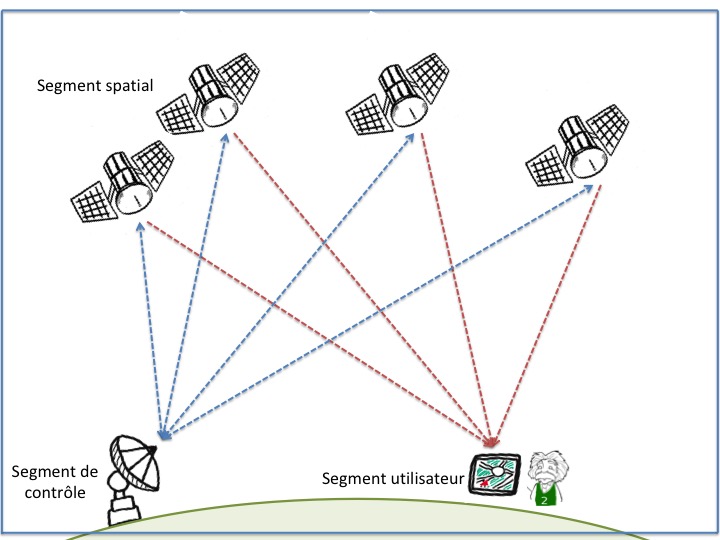
Tous les systèmes de position globale sont organisés autour de trois segments, figure 15 :
- Le segment spatial est formé par l'ensemble des satellites ;
- Le segment de contrôle est assuré par des stations sur Terre. Elles communiquent de façon extrêmement précise avec les satellites pour calculer au plus près leur trajectoire et s'assurer de la position des satellites à chaque instant. La communication a lieu dans les deux sens entre les stations de contrôle et les satellites.
- Le segment utilisateur se réduit à peu de choses. Dans le système GPS l'information n'est que descendante. Les récepteurs sont des systèmes passifs qui reçoivent les signaux. Dans le système Galileo (système de positionnement européen), il y a une possibilité supplémentaire pour émettre des messages de sauvetage (par exemple en mer) instantanément repris par la constellation de satellites et localiser l'appel le plus rapidement possible.
4.2 La constellation de satellites
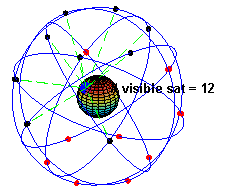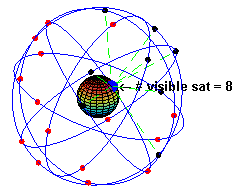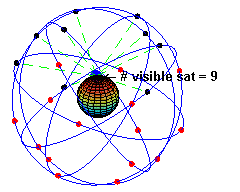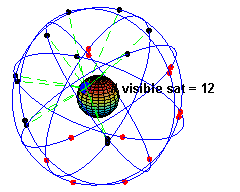
Il est nécessaire qu'en tout point et 24h/24 au moins 4 satellites soient au-dessus de l'horizon et « bien » disposés (occupation d'un volume assez grand) pour avoir une bonne précision.
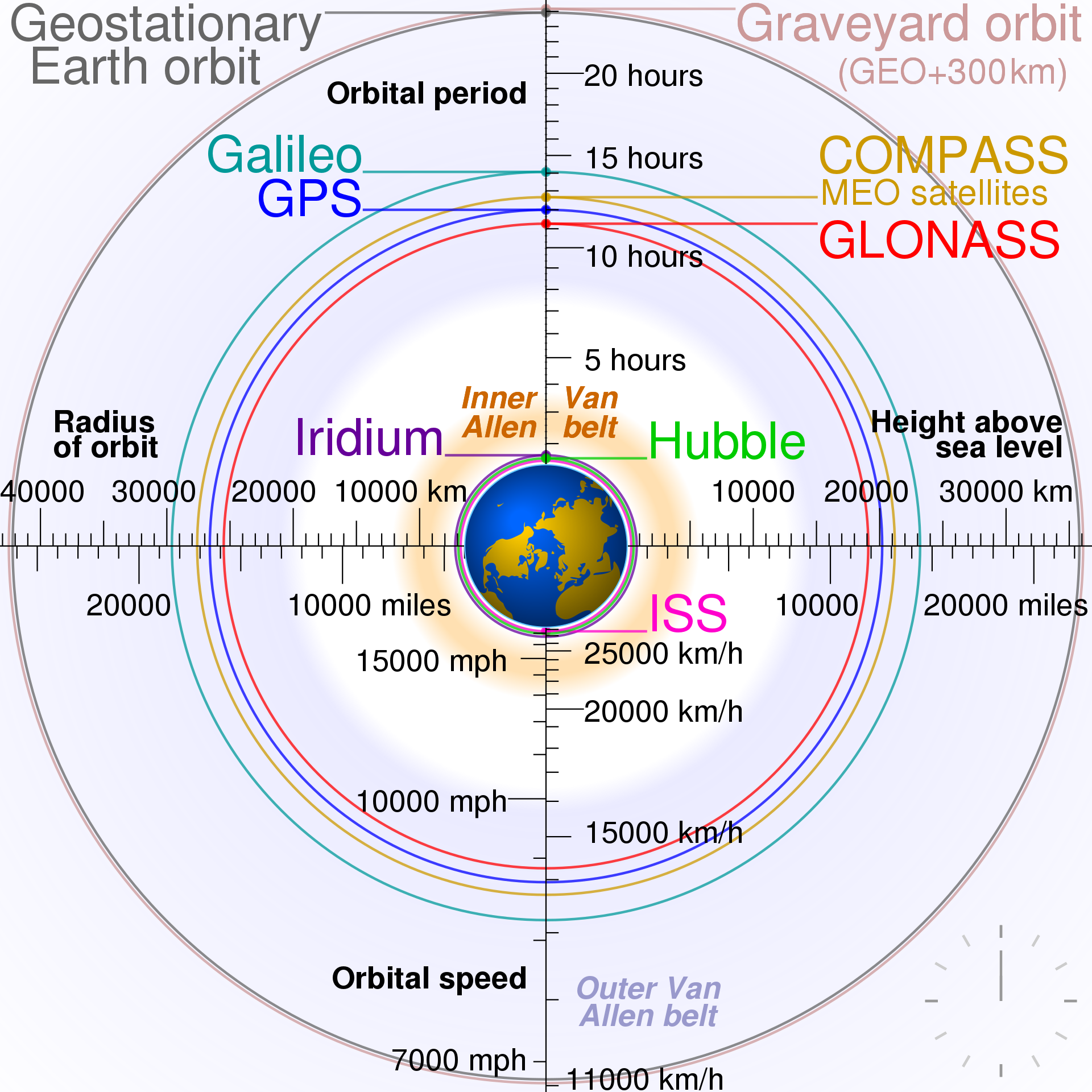
Sur la figure 16 sont représentées les orbites des satellites des différents systèmes de positionnement : GPS pour les États-Unis , Galileo pour l'Europe , GLONASS pour la Russie , Compass ou Beidou pour la Chine
Source : cmglee — Travail personnel, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=16891766. | Source : El pak — Wikimedia. |
Le système GPS est constitué de 24 satellites actifs répartis en 6 plans orbitaux inclinés de 55° sur l'équateur et décalés de 60° entre eux. Ils sont en trajectoire circulaire à 20 200 km d'altitude, figures 16 et 17.
La période de leur trajectoire est de 11h58 min et ils se déplacent avec une vitesse de 3,9 km/s (ou 14 000 km/h).
Pour plus d'information sur la partie pratique du système GPS, on pourra consulter le site : https://www.gps.gov/.
La constellation du système de positionnement Galileo regroupe 30 satellites. Ils sont répartis dans seulement 3 plans orbitaux inclinés de 55° sur l'équateur. Les trajectoires sont quasi-circulaires à 23 200 km d'altitude. La période de la trajectoire est de 14h7 min et leur vitesse est de 3,7 km/s (ou 13 300 km/h).
Pour plus d'information sur la partie pratique du système Galileo, on pourra consulter le site : https://www.gsa.europa.eu/.
Une vidéo de présentation du système Galileo est accessible au lien suivant : https://usegalileo.eu/accuracy-matters/FR
En septembre 2019, le système européen Galileo a atteind le milliard d'utilisateurs de smartphones dans le monde.
5. Conclusion
Pour conclure, avec la mise en place des systèmes de positionnement, il est possible de répondre à des questions que l'homme s'est posé depuis toujours, à savoir « où sommes-nous et quelle heure est-il ? »
D'un point de vue moins philosophique et plus physique, on a pu voir que ces systèmes ne peuvent fonctionner sans prendre en compte l'espace temps relativiste dans lequel nous nous trouvons.
Pour citer cet article :
Le GPS - La physique du GPS (2/2), octobre 2019. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/GPS-2.xml