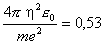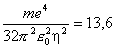Activer le mode zen
Ressource au format PDF
Mots-clés
- énergie
- énergétique
- thermodynamique
- conservation de l'énergie
- entropie
- premier principe
- deuxième principe de la thermodynamique
- équilibre thermodynamique
- système isolé
- transfert d'énergie
- transformation
- joule
- watt
- irréversibilité
- désordre
- interaction fondamentale
Classification
II - Conséquences énergétiques des principes fondamentaux
19/01/2009
Résumé
Le concept d'énergie : principes physiques fondamentaux et hiérarchie des énergies. Deuxième partie du dossier « Les multiples visages de l'énergie », proposé par Roger Balian (première publication le 31 août 2002).
Article précédent : « I - L'élaboration du concept d'énergie »
Article suivant : « III - Comparaisons des différentes formes d'énergie »
Table des matières
Après un exposé historique de l'élaboration du concept d'énergie (voir article « I - L'élaboration du concept d'énergie »), on rappelle, dans la perspective des applications, les principes physiques fondamentaux associés à ce concept : premier principe et deuxième principe de la thermodynamique, dynamique des processus irréversibles, hiérarchie des interactions élémentaires.
L'historique qui précède a mis en évidence quelques uns des apports réciproques de la technologie et de la science dans le domaine de l'énergie. Aujourd'hui, on n'attend plus guère de progrès conceptuels suggérés par l'énergétique, mais à l'inverse celle-ci continuera toujours à reposer sur les données scientifiques. Nous passons ici en revue quatre catégories d'idées sur lesquelles s'appuient toutes les applications pratiques de l'énergie : le premier et le deuxième principe, la thermodynamique hors d'équilibre et la classification issue de la microphysique. Comme tous les autres grands principes de la physique, ces acquis de la science fournissent des contraintes qui limitent les activités humaines.
Premier principe
L'énergie d'un système isolé reste constante au cours du temps (article « I - L'élaboration du concept d'énergie » - partie 3 « Naissance de la thermodynamique »). Il ne peut se créer ni se détruire d'énergie, et il est impropre de parler comme on le fait couramment de « production » ou de « consommation » d'énergie. Dans tous les cas, il s'agit de changement de forme, ou de transfert d'un système à un autre.
Transformations de l'énergie
La vie courante en offre de nombreux exemples. « Consommer » de l'énergie électrique pour faire fonctionner un téléviseur signifie la transformer en énergie lumineuse émise par l'écran (en passant par l'énergie cinétique des électrons issus de la cathode), en énergie acoustique diffusée dans l'air ambiant (par l'intermédiaire des énergies cinétique et potentielle de la membrane du haut-parleur) et surtout en chaleur inutile (principalement par effet Joule).
« Produire » de l'énergie électrique dans une centrale hydroélectrique signifie transformer l'énergie potentielle de l'eau du barrage en énergie cinétique de cette eau dans les conduites, puis transférer cette énergie cinétique aux turbines et au rotor des alternateurs, qui en définitive la transforment en énergie électrique ; la viscosité de l'eau, les frottements et l'effet Joule soustraient de ce flux une faible partie, transformée en chaleur. Dans une centrale thermique, on transforme de l'énergie nucléaire ou chimique en chaleur, puis une partie de celle-ci (30 à 40%) en énergie cinétique, enfin électrique.
De même, dans une voiture, l'énergie chimique du carburant est transformée en chaleur, dont une partie est communiquée au véhicule sous forme d'énergie cinétique ; celle-ci se transforme en chaleur en raison des frottements et de la résistance de l'air, de sorte qu'en définitive lors d'un trajet en circuit fermé on a exclusivement transformé de l'énergie chimique en chaleur ! Lorsqu'on allume les phares, une partie de l'énergie mécanique est transformée successivement en énergies électrique, lumineuse et calorifique, de sorte que la consommation d'essence augmente nécessairement.
Enfin, la biologie fait intervenir des transformations entre énergies de diverses natures : chimique (aliments, métabolisme), radiative (assimilation chlorophyllienne), calorifique, mécanique (muscles), électrique (influx nerveux).
Parmi les diverses formes d'énergie susceptibles de s'échanger les unes en les autres, il convient de distinguer celles qui sont emmagasinées dans la matière de celles qui se manifestent lors d'un transfert d'un sous-système à un autre. A la première catégorie appartiennent l'énergie interne d'un fluide, fonction de sa température et de sa pression, l'énergie chimique d'un carburant, l'énergie nucléaire d'un morceau d'uranium, l'énergie électrochimique d'une batterie, l'énergie potentielle de l'eau d'un barrage dans le champ de pesanteur ou l'énergie cinétique d'un véhicule. La seconde catégorie comprend par exemple la chaleur rayonnée par un radiateur, le travail échangé entre un piston et le fluide qu'il comprime ou l'énergie électrique circulant dans une ligne. La plupart des énergies emmagasinées ne sont accessibles que très indirectement.
Unités
Ces bilans ne peuvent être effectués de façon quantitative que si toutes les formes d'énergie sont mesurées avec la même unité. En principe, on ne devrait utiliser que le joule, unité légale du système international (SI). Dans la pratique, on continue à employer d'autres unités que la tradition a imposées au gré des besoins. Le kilowatt-heure (1 kWh = 3600 kJ) est adapté aux usages domestiques, en particulier à la fourniture d'électricité ; afin de faciliter les comparaisons, le gaz lui aussi n'est plus facturé en France en m3, mais en kWh. Il serait souhaitable, pour permettre au public de mieux apprécier le prix de l'essence et le pouvoir énergétique de ses diverses variétés, de facturer également celle-ci non au litre mais au kWh (la combustion de 1 litre dégage environ 12 kWh de chaleur).
Les chimistes et physiologistes utilisent encore trop souvent l'ancienne unité de chaleur, la kilocalorie (notée aussi Calorie), non légale, qui est la quantité de chaleur à fournir à 1 kg d'eau pour l'échauffer de 1 K ; sa valeur, 1 kcal = 4185 J a été mesurée au XIXème siècle lorsqu'on a établi l'équivalence du travail et de la chaleur.
La microphysique a besoin d'unités d'énergie beaucoup plus petites. L'unité adaptée aux phénomènes de physique atomique ou de physique des solides est l'électron-volt, énergie acquise par un électron lorsque son potentiel électrique diminue de 1 V ; la charge d'une mole d'électrons étant de 96 500 C, on trouve en divisant par le nombre d'Avogadro NA = 6 × 1023 mol-1 que 1 eV = 1,6 × 10-19 J. En physique nucléaire et en physique des particules, on utilise les multiples de 103 en 103 de l'électron-volt : keV, MeV, GeV, TeV. La mécanique quantique associe fréquences et énergies selon la relation E = hν ; un photon au milieu du visible (λ = 0,6 μm) a une fréquence de 0,5 × 1015 Hz, donc une énergie de 2,1 eV. La relation d'Einstein E = mc2 fait correspondre à la masse de l'électron une énergie de 0,511 MeV, ou encore à une masse de 1 μg une énergie de 25 kWh.
Enfin, les économistes et les médias ont malheureusement imposé une unité scientifiquement aberrante, la tonne d'équivalent pétrole (tep ou toe en américain) ainsi que la tonne d'équivalent charbon (1 tec = 0,7 tep). Il s'agit de la quantité de chaleur dégagée par combustion d'une tonne de pétrole, soit 1 tep = 12 MWh ; ce chiffre est approximatif car il dépend de la qualité du pétrole. De plus, lorsqu'on traduit en tep de l'énergie électrique, on tient compte du rendement des centrales thermiques au fioul (38%), de sorte que 1 MWh électrique vaut par convention non 0,1 mais 0,2 tep environ. La nécessité d'utiliser tous ces facteurs de conversion dans la discussion des problèmes énergétiques et dans la comparaison entre formes d'énergie différentes nuit souvent à la clarté du débat.
En ce qui concerne la puissance, ou le flux d'énergie, la situation est plus favorable car c'est l'unité légale, le watt et ses multiples (kW, MW, GW ou TW) qui est la plus couramment utilisée. Les économistes emploient cependant aussi le Tep par an, qui équivaut à 1,4 kW thermique.
Deuxième principe
L'entropie thermodynamique est une grandeur additive que l'on peut associer à chaque état voisin de l'équilibre d'un système. Le deuxième principe peut s'énoncer en exprimant que, pour tout processus spontané, l'entropie d'un système isolé est, dans l'état final, supérieure (ou égale) à sa valeur dans l'état initial (article « I - L'élaboration du concept d'énergie » - partie 3 « Naissance de la thermodynamique »). A l'échelle microscopique, cette propriété traduit une augmentation du désordre (article « I - L'élaboration du concept d'énergie » - partie 5 « L'apport de la physique statistique »). De manière équivalente, elle signifie que l'évolution transfère une information macroscopique sur l'état initial du système vers des degrés de liberté microscopiques inaccessibles, de sorte qu'elle entraîne une perte d'information (article « I - L'élaboration du concept d'énergie » - partie 6 « L'apport de la mécanique quantique, de la relativité et de la physique des particules »). Ces interprétations sont précisées par l'expression S = k ln W de l'entropie, qui la relie au nombre W de configurations microscopiques équivalentes en ce qui concerne l'état macroscopique considéré.
Dans le système SI, l'unité d'entropie est le joule par kelvin, en raison du choix comme unité de température absolue du kelvin, qui est défini en précisant que la température du point triple de l'eau est 273,16 K. La constante de Boltzmann k, qui figure dans l'expression microscopique ci-dessus de l'entropie, vaut alors 1,38 × 10- 23 J.K-1. Il aurait scientifiquement été plus satisfaisant de mesurer les températures en unité d'énergie ; l'entropie aurait alors été une grandeur sans dimension, ce qui est plus conforme à son interprétation microscopique comme mesure du désordre ou du manque d'information. Plus précisément, l'entropie s'identifie à une information manquante si l'on fixe son facteur multiplicatif en la redéfinissant selon S = log2W, ce qui fournit S = 1 pour l'alternative binaire W = 2. Elle se mesure alors en bits, de sorte que le joule par kelvin équivaut à 1,044 × 1023 bits ; ce choix d'unité n'est évidemment pas adapté aux objets macroscopiques, dont le désordre à l'échelle microscopique est gigantesque.
L'entropie S d'un matériau dépend de son énergie interne ainsi que de toutes les autres grandeurs extensives qui caractérisent son état macroscopique. Par exemple, c'est pour un fluide une fonction de l'énergie, du nombre de molécules et du volume. De même que le nombre W de configurations microscopiques, S croît avec l'énergie et avec le volume.
Irréversibilité, dissipation d'entropie et dégradation de l'énergie
Le deuxième principe implique que les processus pouvant survenir dans un système isolé sont en général irréversibles : lorsqu'un certain processus est autorisé, le processus inverse est interdit. Comme le premier principe, le deuxième exprime une limitation de ce que permet la nature. Les processus réversibles, pour lesquels l'entropie reste constante au cours du temps, sont des cas limites, autorisés mais exceptionnels en pratique. Le degré d'irréversibilité d'une transformation d'un système isolé peut être caractérisé par la dissipation, que nous définissons pour plus de généralité comme l'augmentation de son entropie.
Les transformations où l'énergie change de forme doivent en particulier faire croître l'entropie globale (ou éventuellement la laisser constante). Or, l'effet Joule convertit intégralement une énergie électrique en chaleur ; le frottement ou la viscosité convertissent intégralement une énergie cinétique en chaleur. De telles transformations d'énergie électrique ou mécanique en énergie interne sont irréversibles et dissipatives : l'entropie augmente lorsque le système reçoit de la chaleur, parce qu'elle est une fonction croissante de l'énergie interne, alors qu'elle ne dépend pratiquement pas des variables électriques ou mécaniques macroscopiques. Pour cette même raison, les conversions entre une forme ou une autre d'énergie électrique ou mécanique sont des phénomènes réversibles (ou presque) : oscillation d'un ressort ou d'un pendule, auquel cas l'énergie cinétique et l'énergie potentielle (élastique ou de gravité) s'échangent, fonctionnement d'un alternateur ou d'un moteur électrique (où l'effet Joule est faible). De ces observations émerge une nouvelle classification des diverses formes d'énergie. La transformation d'énergie électrique ou mécanique en chaleur apparaît comme une dégradation, car à l'inverse une transformation intégrale de chaleur en énergie électrique ou mécanique est impossible. La chaleur est une forme dégradée d'énergie, les énergies mécaniques et l'énergie électrique sont des formes nobles, équivalentes en ce sens qu'elles peuvent réversiblement s'échanger.
A l'échelle microscopique, cette distinction traduit un caractère plus ou moins désordonné de chaque forme d'énergie. La chaleur s'interprète à cette échelle comme l'énergie cinétique désordonnée, inaccessible à l'observation macroscopique, des particules (molécules pour un fluide, électrons pour un métal). Mais si celles-ci ont un mouvement collectif global, avec une vitesse de dérive d'ensemble qui se superpose aux mouvements désordonnés, isotropes en moyenne, ce mouvement collectif s'observe à notre échelle comme un courant hydrodynamique ou un courant électrique, auquel est associée une énergie ordonnée.
Le mélange (à volume total constant) de deux gaz comportant respectivement M molécules d'un premier type et N molécules d'un second type fait croître le désordre, d'une quantité mesurée par l'entropie de mélange S = k ln[(M+N)!/M!N!]. Ici, il y a dissipation sans phénomène énergétique.
Cependant, la notion de désordre microscopique n'est pas absolue ; elle dépend de nos possibilités d'observation et d'action par des moyens macroscopiques associés à l'information que nous possédons sur le système. Ainsi, le plus souvent, les réactions chimiques libèrent de l'énergie chimique sous forme de chaleur, notamment lorsqu'on utilise des carburants dans les véhicules, les centrales thermiques ou le chauffage domestique. Il faut alors considérer l'énergie chimique (de même que l'énergie nucléaire) comme dégradée. Mais ce n'est pas toujours le cas, car on sait dans certaines circonstances (accumulateurs ou piles) convertir directement et quasi réversiblement de l'énergie chimique en énergie électrique, ce qui conduit alors à considérer l'énergie chimique comme noble.
Bilan d'énergie et d'entropie
Bien des entreprises humaines visent à contrecarrer la tendance naturelle vers le désordre qu'exprime le deuxième principe. Il est évidemment impossible d'y parvenir si le système d'intérêt est isolé. C'est pourquoi il faut coupler ce système avec des sources, autres systèmes avec lesquels il peut interagir. Son entropie peut ainsi décroître dès lors que les sources sont le siège d'un accroissement au moins égal d'entropie. On exploite de la sorte la tendance globale du système composite à évoluer vers un état d'entropie plus grande, afin de faire localement décroître l'entropie du sous-système d'intérêt.
Si par exemple on souhaite refroidir un système A, il doit pour satisfaire au premier principe céder une certaine quantité de chaleur δ Q = - δ UB = - δ UA > 0 à une source B. Ceci implique que son entropie décroisse ( δ SA < 0 ) en même temps que son énergie, en vertu de la définition
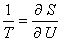 (équation 1)
(équation 1)
de la température absolue (On suppose fixées les variables extensives autres que l'énergie, telles que le volume et le nombre de particules). Il est donc nécessaire que, selon le deuxième principe, l'entropie de B croisse au cours du processus d'une quantité δ SB supérieure à |δ SA|, ce qui implique
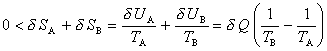
et par suite TA > TB. Le système A ne peut donc se refroidir que s'il a une température plus élevée que celle de la source B, énoncé de Clausius du deuxième principe.
Cet exemple montre l'utilité dans les questions d'énergétique d'un double bilan traduisant mathématiquement les deux principes. Etant donné un ensemble de sous-systèmes interagissant les uns avec les autres, la variation d'énergie de chacun d'eux doit être égale à l'énergie qu'il reçoit, tandis que sa variation d'entropie doit être supérieure à l'entropie qu'il reçoit. Ces égalités et inégalités fournissent des contraintes sur les processus réalisables.
Ici encore, la vie courante fournit de nombreuses illustrations. Si une cuisine contenant un réfrigérateur était isolée de l'extérieur, il serait impossible de refroidir l'intérieur A du réfrigérateur par transfert de chaleur à l'air B de la cuisine, car la transformation inverse, qui se produit spontanément, est irréversible ; mathématiquement, la conservation de l'énergie totale impliquerait pour ce processus une décroissance de l'entropie puisque TA < TB. On ne peut faire fonctionner le réfrigérateur, en abaissant son énergie intérieure de |δUA| , que grâce à un apport δW d'énergie fournie de l'extérieur sous forme électrique et transformée en énergie mécanique dans le bloc compresseur. Le double bilan, d'énergie et d'entropie, fournit alors :
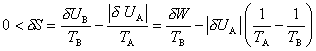
ce qui détermine la consommation minimale d'énergie électrique δW de l'appareil. Un calcul complet, qui fournirait la puissance minimale du réfrigérateur, nécessite la prise en compte du flux de chaleur à travers les parois. La même estimation est valable pour un climatiseur.
Le même bilan s'applique à une pompe à chaleur, qui a pour but de transférer de la chaleur depuis l'air extérieur A, froid, vers l'intérieur B d'une habitation afin de la chauffer. Etant donné qu'un tel flux va en sens inverse de celui que prévoit l'énoncé de Clausius, son établissement nécessite la consommation (dans un appareillage analogue à celui d'un réfrigérateur) d'une certaine quantité d'énergie mécanique ou électrique δW, dont la valeur minimale se calcule comme ci-dessus. La quantité d'intérêt est cependant ici la chaleur δUB cédée à l'habitation, et non celle extraite de la source froide (l'extérieur). Le rendement maximal est ainsi donné par
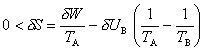
ce qui montre que l'énergie δW consommée par la pompe à chaleur peut être très inférieure à la valeur δUB que l'on aurait consommée en utilisant par exemple un radiateur électrique : à l'énergie électrique δW utilisée s'est ajoutée la chaleur | δUA | tirée de l'extérieur. On peut imaginer de même, en ne considérant que des sources de chaleur, que l'on souhaite chauffer un local B à l'aide d'une chaudière C à température élevée. Pour une quantité δUB de chaleur fournie au local, il est possible d'économiser la chaleur | δUC | cédée par cette chaudière en l'utilisant non directement, mais pour faire fonctionner une pompe à chaleur branchée sur l'air extérieur A, à température plus basse (TA < TB < TC). La chaudière est alors la source chaude d'un générateur d'électricité alimentant la pompe à chaleur. Le bilan global d'énergie indique que la quantité de chaleur reçue par le local B comprend non seulement la chaleur fournie par la chaudière C, mais aussi celle extraite de l'air extérieur A. Le bilan d'entropie de A, B et C,
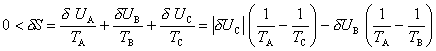
montre que l'on peut espérer pour borne supérieure du rendement global une valeur très supérieure à 1 ; on peut gagner par exemple jusqu'à un facteur 10 lorsque TA = 0°C, TB = 20°C, TC = 600°C grâce à cette utilisation indirecte de la chaudière.
Inversement, la production d'une énergie mécanique ou électrique δW par un moteur thermique ou une turbine nécessite évidemment une source A d'énergie, la source chaude dont l'énergie UA doit diminuer. Mais cette diminution implique aussi une diminution ( δSA < 0) de l'entropie SA, diminution qui doit être compensée par la croissance de l'entropie SB d'un autre sous-système B. Ce dernier n'est autre que la source froide du moteur, qui est en réalité une source de neguentropie nécessaire à la satisfaction du double bilan ; la chaleur que cette source reçoit doit faire croître SB d'une quantité δSB supérieure à |δSA|, ce qui implique
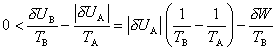
inéquation qui détermine le rendement maximalδW / |δUA| du moteur, comme l'avait déjà vu Carnot (article « I - L'élaboration du concept d'énergie » - partie 3 « Naissance de la thermodynamique »).
Dans bien des cas, l'énergie n'est pas la seule quantité conservative en jeu, et les sous-systèmes peuvent échanger d'autres grandeurs, par exemple des particules de tel ou tel type, notamment en chimie. Ils peuvent aussi échanger du volume, lorsque l'un des sous-systèmes se dilate aux dépens d'un autre. En pareils cas, les bilans doivent tenir compte de toutes ces grandeurs conservés. Par exemple, le dessalement de l'eau de mer nécessite une décroissance de son entropie, puisque la dissolution du sel dans de l'eau est un phénomène irréversible où la dissipation est égale à l'entropie de mélange. Cette opération n'est rendue possible que grâce à un apport d'énergie, calorifique, mécanique ou électrique selon le procédé utilisé, apport permettant de faire croître l'entropie des sources extérieures d'une quantité supérieure à la baisse de l'entropie de mélange. De même, la croissance d'ordre associée au développement d'un être vivant nécessite une croissance d'entropie de son environnement, accompagnant des transferts d'énergie et de molécules diverses.
Enfin, l'équivalence entre manque d'information et entropie, mise en évidence par Brillouin, implique que l'enregistrement dans une mémoire d'une information doit s'accompagner, ici encore, d'une croissance d'entropie de l'environnement.
Principes de la thermodynamique hors équilibre
Les principes de la thermodynamique traditionnelle, rappelés précédemment, ne portent que sur des états de quasi équilibre. Grâce à la comparaison de l'état initial et de l'état final, ils permettent de faire un bilan des divers processus, et fournissent ainsi une borne théorique supérieure aux rendements. Mais ils ne donnent aucune indication sur les rendements réels, qui dépendent de la valeur de la dissipation totale. D'autre part, on est souvent intéressé dans les questions énergétiques, non seulement par l'énergie mais aussi par la puissance. Or, la thermodynamique traditionnelle ne nous renseigne pas sur le déroulement des processus dans le temps, sur lequel reposent les technologies. Comme nous l'avons signalé à la fin de la partie 4 « La thermodynamique des processus irréversibles », article « I - L'élaboration du concept d'énergie », les lois qui régissent ces processus dynamiques, qu'ils soient mécaniques, thermiques, électriques ou chimiques, obéissent à des principes communs, tout au moins lorsque les états successifs du système restent voisins de l'équilibre. Nous allons passer sommairement ces principes en revue, en les illustrant à l'aide de l'exemple historique du problème de la chaleur (début de la partie 3 « Naissance de la thermodynamique », article « I - L'élaboration du concept d'énergie ») reformulé dans le langage de la théorie générale. On pourra en première lecture survoler la sous-partie suivante.
Les équations dynamiques
Lorsque de la chaleur se propage dans un milieu solide, la seule grandeur transportée est l'énergie. L'état du système à chaque instant est caractérisé par la valeur ρE d3r de l'énergie (qui se réduit ici à l'énergie interne) dans chaque élément de volume ; le but est d'étudier l'évolution de la densité d'énergie ρE ( r , t ). Dans un problème général, l'état de chaque élément de volume (ou de chaque sous-système homogène) est caractérisé à chaque instant par la donnée d'un certain nombre de variables extensives conservatives locales qui peuvent comprendre l'énergie, la quantité de mouvement, le volume, ou le nombre de particules de tel ou tel type, et que nous désignerons par ρ i.
A ces variables d'état sont associées des variables intensives locales, température, vitesse hydrodynamique, pression, potentiels chimiques. Etant donné que chaque élément de volume est presque à l'équilibre, ces variables intensives s'expriment en fonction des précédentes à l'aide des mêmes équations d'état qu'en thermodynamique d'équilibre. Dans le cas particulier du problème de la chaleur, l'équation d'état est la relation (1) entre densité d'énergie et température. Plus généralement, les équations d'état peuvent s'obtenir systématiquement en dérivant l'entropie par rapport aux variables extensives (comme l'énergie ou le volume). Il est donc naturel dans le présent contexte de choisir comme variable intensive γi conjuguée de la variable ρi la dérivée partielle de la densité d'entropie s par rapport à la densité ρi ; ceci conduit en particulier à caractériser la température locale par la variable :
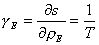 (équation 2)
(équation 2)
inverse de la température absolue. (De même, la variable intensive γN associée au nombre de particules d'un certain type est - μ / T, où μ est le potentiel chimique de ces particules.)
Lorsque le système entier est à l'équilibre global, la température est uniforme. L'écart à l'équilibre est donc caractérisé par la donnée en chaque point du gradient de la température, c'est-à-dire de ∇ γE = - ∇ T / T2, et plus généralement de grandeurs appelées affinités, du type ∇γi. (Pour un système constitué de sous-systèmes pratiquement homogènes, comme l'air d'une pièce et le radiateur qui le chauffe, l'affinité thermique est définie comme la différence de leurs variables intensives γE = 1 / T ; pour un conducteur électrique isotherme, l'affinité ∆ γN est proportionnelle au gradient ∆μ du potentiel électrochimique des porteurs de charge, c'est-à-dire à la force électromotrice ; pour une réaction chimique, l'affinité est la combinaison linéaire des potentiels chimiques qui s'annule à l'équilibre ; de part et d'autre d'un piston mobile, l'affinité associée au volume est la différence des pressions divisée par la température.)
Le déroulement des processus dans le temps est gouverné par le taux de transfert, d'un sous-système à l'autre, des grandeurs conservatives. Dans l'exemple ci-dessus du chauffage domestique, ce taux est mesuré par le flux de chaleur passant du radiateur à l'air de la pièce à travers la surface qui les sépare. Dans le cas général, des flux de chaleur peuvent exister pour toute paire de sous-systèmes voisins (entre l'air de la pièce et les murs ou les fenêtres, entre celles-ci et l'air extérieur) ; on doit aussi considérer des flux pour les autres grandeurs conservatives, flux de quantité de mouvement ou de particules (par exemple flux d'air sous une porte). Selon la version dynamique du premier principe, la dérivée par rapport au temps de l'énergie d'un sous-système est égale à la somme des flux d'énergie qu'il reçoit de ses voisins. Le même type de relation existe pour toutes les autres grandeurs conservatives. Pour un milieu continu, les flux à travers une surface sont engendrés comme des intégrales de surface des densités de courantJi ; par exemple, la densité de courant d'énergie JE est un champ de vecteurs qui se réduit pour un milieu solide à la densité de courant de chaleur. Le flux de chaleur sortant d'un élément de volume infinitésimal d3r vaut div JE d3 r. Le bilan pour chaque élément de volume des lois de conservation se traduit par une équation locale du type
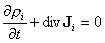 (équation 3)
(équation 3)
en particulier avec i = E pour le problème de la chaleur ou avec i = N pour la conservation du nombre de particules en dynamique des fluides. (En chimie, le flux associé à une réaction est défini comme la vitesse à laquelle cette réaction se produit ; en mécanique, la flux de quantité de mouvement s'identifie au tenseur des contraintes.)
Les équations dynamiques sont complétées par un dernier ensemble de relations, qui permettent d'exprimer les flux en fonction des affinités. L'exemple le plus simple est la loi de Fourier (article « I - L'élaboration du concept d'énergie » - partie 3 « Naissance de la thermodynamique ») :
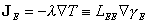 (équation 4)
(équation 4)
où λ est la conductibilité calorifique, et où LEE ≡ λ T2. La forme de cette relation est intuitive. En effet, à l'équilibre global, les flux de chaleur s'annulent avec les gradients de température ; un écart de température entre un point et un autre provoque un courant de chaleur qui tend à réduire cet écart. Dans un régime suffisamment proche de l'équilibre, ce courant est selon (4) proportionnel à la perturbation ∇ γE. Nous avons passé en revue à la partie 4 « La thermodynamique des processus irréversibles », article « I - L'élaboration du concept d'énergie » un grand nombre de phénomènes régis par des lois analogues à (4). De Donder a posé en principe général que les flux (ou les densités de courant) sont proportionnels aux affinités, selon
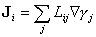 (équation 5)
(équation 5)
Les coefficients de réponseL expriment la manière dont le système « répond », grâce à un transport des grandeurs conservatives, aux déviations par rapport à l'équilibre. Ils caractérisent la dynamique proprement dite ; ils n'apparaissent pas dans la « thermodynamique » traditionnelle qui, malgré son nom, concerne seulement les états d'équilibre caractérisés par des équations d'état du type (2), ainsi que les déplacements d'équilibre décrits par différentiation de ces équations.
L'équation de la chaleur résulte en définitive de (2), (3) et (4), qui donnent :
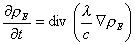 (équation 6)
(équation 6)
où c est la chaleur spécifique par unité de volume du solide. Dans le cas général, les équations du mouvement s'obtiennent en combinant les équations de réponse semi-empiriques (5), dont de nombreux exemples ont été donnés à la partie 4 « La thermodynamique des processus irréversibles », article « I - L'élaboration du concept d'énergie », aux équations d'état (2) et aux équations de conservation (3).
Plusieurs principes, que la physique statistique permet de déduire de la structure microscopique du matériau considéré (article « I - L'élaboration du concept d'énergie » - partie 5 « L'apport de la physique statistique »), fournissent des contraintes sur ses coefficients empiriques de réponse L. Le principe de Curie exprime que les symétries du matériau, c'est-à-dire le fait qu'il reste ou non invariant sous l'effet de telle ou telle translation, de telle ou telle rotation, ou lorsqu'on prend son image dans un miroir, se reflètent sur les coefficients L. Ainsi, dans la relation (4), LEE représente a priori une matrice 3 × 3 reliant les composantes du vecteur JE à celles de ∇γE. Pour un matériau isotrope ou encore pour un cristal ayant les symétries du cube, cette matrice doit être proportionnelle à l'unité, de sorte que LEE (ou λ) est un scalaire. Pour d'autres symétries cristallines, la matrice LEE peut avoir plusieurs composantes indépendantes, avec une structure déterminée par le groupe cristallin.
Le principe d'Onsager se traduit par des relations du type Lij = Lji ou Lij = – Lji, qui associent l'une à l'autre des propriétés résultant de l'échange des causes et des effets. Par exemple, pour les effets thermoélectriques (article « I - L'élaboration du concept d'énergie » - partie 4 « La thermodynamique des processus irréversibles »), le coefficient LEN, qui régit le courant de chaleur induit par un gradient de potentiel électrochimique (effet Peltier), est égal au coefficient LNE, qui régit le courant électrique engendré par un gradient thermique (effet Seebeck). Les relations d'Onsager sont une conséquence de l'invariance par renversement du temps des équations dynamiques à l'échelle microscopique.
Taux de dissipation
Un dernier principe concerne la dissipation. Pour un flux de chaleur, on tire de (2), (3), puis (4) la variation par rapport au temps de la densité d'entropie s ( r ,t) :
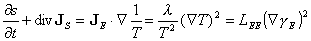 (équation 7)
(équation 7)
où JS ≡ JE / T définit la densité de courant d'entropie. La comparaison avec (4) montre que l'entropie n'est pas conservative, et que son taux de création par unité de temps et par unité de volume, ou taux de dissipation, est exprimé par le second membre de (7). Plus généralement, le taux de dissipation de tout processus assez proche de l'équilibre est donné par l'équation de bilan détaillé temporel :
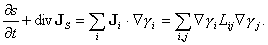 (équation 8)
(équation 8)
Le dernier principe de la thermodynamique hors d'équilibre est alors exprimé par l'inégalité de Clausius–Duhem, selon laquelle l'expression (8) est en toutes circonstances positive (ou éventuellement nulle). Cette propriété est apparentée au deuxième principe de la thermodynamique traditionnelle, mais ne coïncide pas avec lui. Celui-ci, moins détaillé, se réfère en effet seulement à l'état initial et l'état final, et non au déroulement du processus dans le temps ; en revanche, il est plus général car il ne suppose pas que le processus soit voisin de l'équilibre. La positivité de (8) implique des inégalités sur les coefficients de réponse L, par exemple λ >0. Dans cette équation, le courant JS décrit un transport d'entropie d'un point à l'autre, il s'y superpose une création d'entropie en chaque point, proportionnelle au carré des flux ou des affinités. La dissipation totale associée à un processus est l'intégrale du second membre de (8) sur le volume du système et sur la durée du processus.
Ce résultat est important pour les applications à l'énergétique. En effet, si le principe de Carnot établit l'existence d'un rendement maximal pour un processus (partie « Deuxième principe »), le rendement réel peut être nettement inférieur ; il dépend des phénomènes physiques et des dispositifs utilisés, et aussi du temps τ mis pour réaliser le processus. Pour un système donné, si l'on cherche en un temps τ à transférer d'un sous-système à un autre une grandeur donnée, par exemple en convertissant une certaine quantité d'énergie d'une forme en une autre, les flux doivent être inversement proportionnels à la durée τ du processus, J µ 1/ τ . Il en est de même des affinités, Ñ γ µ 1/ τ . Il résulte de (8) que le taux de dissipation est proportionnel à 1 / τ2, et donc que la dissipation totale est proportionnelle à 1 / τ . Ainsi, plus on cherche à réaliser une action rapidement, plus son irréversibilité est grande ; les transformations réversibles, ayant le meilleur rendement possible, sont infiniment lentes. Les équations ci-dessus permettent d'estimer le véritable rendement. Ceci généralise une observation courante : du fait de la résistance de l'air, la consommation d'essence d'une voiture au kilomètre croît avec la vitesse.
Toute réalisation technologique nécessite en définitive un compromis entre l'amélioration du rendement (dans les limites imposées par le deuxième principe) et le raccourcissement de la durée du processus. Un exemple extrême est celui de l'enrichissement de l'uranium par diffusion gazeuse : l'usine de Pierrelatte consomme, pour pomper l'hexafluorure d'uranium gazeux à travers les barrières poreuses qui laissent mieux passer l'isotope 235 que l'isotope 238, une énergie mécanique de 9 MWh par kg d'uranium enrichi, ce qui représente 7 × 107 fois plus que le minimum théorique imposé par la diminution de l'entropie de mélange !
Hiérarchie des énergies
La microphysique a mis en évidence l'existence de quatre interactions fondamentales entre particules élémentaires (article « I - L'élaboration du concept d'énergie » - partie 6 « L'apport de la mécanique quantique, de la relativité et de la physique des particules »). Même si la théorie est parvenue à les unifier partiellement, elles ont des propriétés très différentes qui se reflètent sur les énergies qui leur sont associées à l'échelle macroscopique. Nous les passons en revue par ordre d'intensités décroissantes, ce qui fournit encore une nouvelle classification des énergies.
Interaction forte
L'interaction la plus intense, dite forte, est responsable de la cohésion des noyaux. Elle est en jeu dans la radioactivité α et dans la plupart des réactions nucléaires. Elle attire entre eux les nucléons (protons et neutrons). Sa portée est de l'ordre du femtomètre (1 fm = 10-15 m), et son intensité est de l'ordre de 1 à 10 MeV, ordre de grandeur de l'énergie de liaison d'un nucléon dans un noyau.
Cette énergie est suffisamment forte pour qu'on puisse l'observer, selon la formule E = mc2 , sous forme de masse. En effet, les masses atomiques ne sont pas exactement proportionnelles au nombre de protons et de neutrons, et le défaut de masse mesure l'énergie de liaison, à raison d'environ 1 mg.mol-1 pour 1 MeV. Ce chiffre, calculé à l'aide des facteurs de conversion de la partie « Premier principe » - sous-partie « Unités », est une fraction significative de la masse atomique (1 g.mol-1 pour H). L'énergie de liaison par nucléon est maximale au milieu du tableau de Mendeleïev : d'environ 8,5 MeV pour un nombre de masse 30 < A < 120 elle tombe à 7,5 MeV pour A > 220 ; elle croît de 1 MeV à 7 MeV entre 2H et 4He. On peut donc récupérer de l'énergie (calorifique) par réactions soit de fission de noyaux lourds (U, Pu, Th) dans un réacteur, soit de fusion menant à 4He.
L'énergie solaire, qui quitte le Soleil sous forme de rayonnement électromagnétique, est engendrée dans son cœur par des réactions de fusion successives transformant l'hydrogène en hélium. Les recherches sur la fusion contrôlée ne reposent pas sur ces réactions, impossibles à réaliser, même en laboratoire, mais sur la fusion du deutérium 2H et du tritium 3H ; le premier peut être extrait de l'eau de mer, le second doit être produit par fission du lithium.
Interaction électromagnétique
L'interaction coulombienne est à la base de très nombreux phénomènes énergétiques. En raison de son comportement en 1/r, elle se manifeste avec deux intensités différentes.
A l'intérieur des noyaux, où les distances entre nucléons sont de l'ordre du fm, l'interaction coulombienne e2 / 4πε0 r entre deux protons, répulsive, est de l'ordre du MeV. Elle est donc significative devant l'interaction forte. Elle est responsable, lorsque les noyaux deviennent de plus en plus lourds, de la décroissance de leur énergie de liaison puis de leur instabilité. Elle constitue le principal obstacle à la réalisation de la fusion contrôlée, car elle s'oppose au rapprochement des noyaux chargés jusqu'à une distance égale à la portée de l'interaction forte susceptible de les lier. Afin de la surmonter, il faut communiquer aux noyaux une énergie cinétique relative importante, grâce à une élévation considérable de la température (107 K dans le cœur du Soleil) et de la densité. Enfin, elle intervient dans la radioactivité γ.
Cependant, pour toutes les autres applications à l'énergétique, les distances entre particules chargées, noyaux ou électrons, sont de l'ordre de l'angström (10-10 m = 0,1 nm), et leurs énergies coulombiennes caractéristiques sont donc de l'ordre de l'électron-volt. En effet, les phénomènes à l'échelle atomique sont gouvernés par l'interaction coulombienne et par la physique quantique qui régissent la dynamique des électrons (ainsi que celle des noyaux, mais ceux-ci, beaucoup plus lents, contribuent beaucoup moins à l'énergie). Les seules constantes fondamentales et données physiques qui apparaissent dans ce problème sont e, ε0, η et la masse m de l'électron (la constante c, par exemple, ne peut intervenir car les vitesses en jeu ne sont pas relativistes). La seule grandeur ayant une dimension de longueur que l'on puisse construire avec ces constantes est, à une constante numérique près,
|
le rayon de Bohr de l'atome d'hydrogène. De même, la seule énergie est :
|
l'énergie de liaison de l'atome d'hydrogène. Ces chiffres apparaissent comme conséquence de la compétition entre attraction coulombienne et tendance à l'étalement imposée par la physique quantique. Dans les molécules et les solides, dont les propriétés sont aussi gouvernées principalement par les électrons, les ordres de grandeur sont les mêmes : les distances entre noyaux sont encore de quelques angströms, et les énergies de liaison typiques de 0,1 eV à quelques eV par atome.
Ces ordres de grandeur se reflètent à notre échelle dans de nombreuses énergies d'usage courant, qui sont dominées à l'échelle microscopique par l'interaction électrique ou plus généralement électromagnétique. L'énergie chimique, libérée par exemple par une combustion, n'est autre qu'une variation d'énergie coulombienne et cinétique associée au réarrangement des molécules. Rapportée à une mole, une énergie par particule de 1 eV conduit à 96,5 kJ mol-1, c'est-à-dire 27 Wh mol-1 ou 23 kcal mol-1 (partie « Premier principe » - sous-partie « Unités »). On vérifie que la chaleur de combustion du pétrole (1 tep = 12 MWh) correspond bien à quelques dizaines d'eV par molécule (plus précisément 0,45 eV fois la masse molaire moyenne en g mol-1). D'autres réactions chimiques que les combustions donnent en général des chiffres plus faibles quoique comparables. Par exemple, en électrochimie, la force électromotrice typique d'une pile, 1 à 3 V, indique que la variation d'énergie d'un électron est de 1 à 3 eV lorsqu'il passe d'une électrode à l'autre. La même valeur se retrouve pour la largeur typique d'une bande interdite de semi-conducteur, paramètre essentiel pour les photopiles et tous les dispositifs électroniques. En biochimie, la source d'énergie des processus intracellulaires est l'hydrolyse de l'ATP en ADP (adénosine tri- et diphosphate), réaction qui dégage 0,5 eV par molécule ou 50 kJ par mole. Dans un organisme humain, 40 kg d'ATP sont ainsi transformés chaque jour, ce qui nécessite une régénération permanente d'ADP en ATP par consommation de glucose fourni par l'alimentation ; ce chiffre est en accord avec la puissance moyenne absorbée sous forme d'aliments, 2700 kcal par jour ou 130 W.
La cohésion des solides est analogue à la liaison des molécules. En conséquence, leur énergie élastique, par exemple celle d'un ressort tendu, leur énergie calorifique, qui reflète à notre échelle les vibrations du réseau cristallin ou dans un métal les mouvements des électrons, sont de nature électromagnétique. La valeur de l'énergie de liaison peut s'estimer à l'aide des chaleurs de fusion et de vaporisation, par exemple pour l'eau 0,06 eV (correspondant à 80 cal g-1) et 0,1 eV par molécule, chiffres encore en accord avec les ordres de grandeur ci-dessus.
Bien entendu, l'énergie électrique macroscopique se rattache directement à l'interaction électromagnétique microscopique, qu'elle met en évidence à notre échelle grâce à des mouvements collectifs de charges élémentaires ou à des densités de charge macroscopiques. Les unités électriques usuelles traduisent d'ailleurs les ordres de grandeur de la microphysique. A l'énergie de 1 eV pour un électron correspond une différence de potentiel de 1 V. La charge de NA électrons est le faraday, qui vaut 96 500 C ; ce rapport de l'ordre de 105 traduit le fait que seule une faible fraction des électrons ou des ions est mobile dans un conducteur
Il faut souligner dans ce contexte l'importance technologique du magnétisme et surtout du ferromagnétisme, sans lequel nous n'aurions ni alternateurs, ni moteurs, ni transformateurs, ni donc lignes à haute tension. Il est intéressant de noter que le magnétisme, propriété essentielle pour notre emploi quotidien de l'électricité, n'existerait pas en physique classique : il ne s'explique à l'échelle microscopique que grâce à la physique quantique.
Enfin, l'énergie radiative (solaire, ou émise par une lampe électrique, ou transformée en chaleur dans un four micro-ondes) est aussi de nature électromagnétique. Ici encore, on retrouve l'énergie caractéristique de 2 eV, qui est celle d'un photon de 0,6 µm au milieu du visible (partie « Premier principe » - sous-partie « Unités »). Les plantes se sont adaptées à cette valeur, puisque l'énergie caractéristique de l'assimilation chlorophyllienne est du même ordre. En effet, la fixation d'une molécule de CO2 atmosphérique sur une molécule d'eau pour donner un chaînon glucidique – CHOH – et de l'oxygène nécessite un apport d'énergie de 5 eV (correspondant à 500 kJ.mol-1) fourni par le flux lumineux.
Interaction faible
Beaucoup moins intense que l'interaction électromagnétique, l'interaction dite faible est responsable de la radioactivité β. Les énergies qu'elle met en jeu sont de l'ordre d'une fraction de MeV, donc appréciables même en tant que variations de masse, comme pour l'interaction forte. Sa faiblesse se traduit par une probabilité extrêmement petite des processus qu'elle gouverne. Elle n'intervient dans les questions énergétiques qu'en une circonstance, cachée mais importante. Parmi les réactions nucléaires successives qui libèrent l'énergie solaire, la réaction initiale est la fusion de deux protons en un deutéron (plus un positon et un neutrino). Contrairement aux réactions ultérieures qui mènent en définitive au noyau d'hélium, cette fusion est un processus faible, donc très peu probable. Elle est d'ailleurs inobservable en laboratoire. Elle constitue pour la dynamique des réactions de fusion un goulot d'étranglement qui rend très lente la transformation d'énergie nucléaire en chaleur dans le Soleil : la production de chaleur dans le cœur du Soleil (qui représente 1/3000 de son volume) n'est que de 800 W.m-3, à comparer au dégagement de chaleur par le corps humain, 100 W au repos (dont 20 % pour le fonctionnement du cerveau), 500 W en activité physique. C'est cette petitesse qui permettra au Soleil de rayonner pendant une dizaine de milliards d'années.
Interaction gravitationnelle
L'interaction gravitationnelle est la plus faible des quatre interactions fondamentales. Sa forme, -GMM'/r pour deux masses M et M', est semblable à celle de l'interaction coulombienne. Mais la constante de gravitation vaut G = 6,67 × 10-11 J.m.kg-2, de sorte que l'attraction gravitationnelle entre deux protons est 8 × 10-37 fois plus faible que leur répulsion coulombienne. Cette attraction devient sensible à notre échelle grâce à la grande masse des objets en jeu. En particulier, c'est la masse de la Terre qui engendre le potentiel de gravité, source de l'énergie hydroélectrique. Les unités SI sont adaptées à ce phénomène, puisque la chute de 1 kg d'eau sur 1 m lui communique une énergie cinétique de 9,8 J = 2,7 mWh, faible devant le kWh, énergie caractéristique associée pour 1 kg de matière à l'interaction électromagnétique.
L'énergie cinétique macroscopique, mise en œuvre dans une turbine ou une éolienne, s'apparente à l'énergie potentielle gravifique de point de vue des ordres de grandeur. De fait, énergies cinétique et potentielle s'échangent presque réversiblement (aux effets de viscosité près) dans une usine hydroélectrique. Sur le plan théorique, gravitation et mouvement sont d'ailleurs unifiés par la relativité générale. (L'énergie cinétique microscopique, qui se traduit dans un gaz par son énergie interne, a un ordre de grandeur plus élevé, s'approchant de celui des énergies chimiques.)
La gravitation, comme les autres interactions, joue un rôle dans le fonctionnement du Soleil en tant que machine énergétique. Une élévation accidentelle de température a pour effet d'augmenter le taux de fusion nucléaire, donc d'accroître la production d'énergie. Si cette énergie excédentaire se transformait en chaleur, la température augmenterait encore, ce qui ferait en définitive exploser notre étoile ! A l'inverse, un refroidissement local serait amplifié par la baisse résultante du taux de réaction, jusqu'à l'extinction du Soleil. C'est la gravitation qui fournit un remarquable mécanisme de stabilisation du flux d'énergie solaire. On montre en effet que l'équilibre entre forces de pression et de gravité à l'intérieur du Soleil implique que son énergie totale, négative, est la moitié de son énergie gravitationnelle, donc l'opposée de son énergie interne. Un accroissement de l'énergie totale provoque donc, grâce à la dilatation du Soleil qui l'accompagne, une diminution égale de l'énergie interne, donc une baisse de température, ce qui ramène le taux de conversion d'énergie nucléaire en chaleur à sa valeur stationnaire.
Article précédent : « I - L'élaboration du concept d'énergie »
Article suivant : « III - Comparaisons des différentes formes d'énergie »
Dossier : « Les multiples visages de l'énergie »
Pour citer cet article :
Conséquences énergétiques des principes fondamentaux, Roger Balian, janvier 2009. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Consequences-energetiques-principes-fondamentaux-Balian.xml