Propagation des sons

On se limite à une propagation unidimensionnelle de l’onde sonore.

Figure 2. Modélisation 1D de la propagation d'une onde sonore créée par un diapason - Extrait de la source : Acoustics: "Sound Waves And Their Sources" 1950 Encyclopaedia Britannica Films; Physics of Sound

Figure 3. Schéma de la propagation en une dimension d'une onde sonore, selon Ox

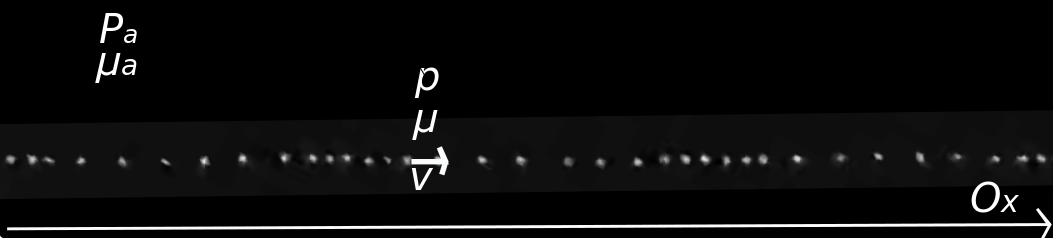
Soit P_a la pression du fluide à l’équilibre et μ_a sa masse volumique (figure 3). En présence d’une onde sonore, la pression dans le fluide devient, dans la direction de l’axe (Ox) :

$P(x,t)=P_a+p(x,t)$

avec p(x,t) la surpression acoustique. Cette surpression reste toujours faible vis-à-vis de la pression atmosphérique. Par exemple, pour l’air, elle vaut 2 mPa dans une pièce calme et peut atteindre quelques dizaines de pascals lors du décollage d’un avion.

La masse volumique du fluide varie également faiblement autour de sa position d’équilibre, d’une quantité que l’on notera μ(x,t), de telle sorte que la masse volumique totale du fluide sera :

${\mu }_{Tot(x,t)}={\mu }_a+\mu (x,t)$

En considérant initialement l'air au repos, la vitesse d'une tranche de fluide est égale à la vitesse v(x,t) de la perturbation.

L’expérience montre que la propagation des ondes sonores est généralement caractérisée par un faible amortissement au sein du fluide où elles se propagent. On néglige donc les phénomènes dissipatifs (comme la conduction thermique ou les phénomènes de viscosité), ce qui revient à postuler le caractère isentropique de la propagation des ondes sonores.

La conservation géométrique de l'énergie implique que l'intensité sonore décroit lorsqu'on séloigne de la source.

Le coefficient de compressibilité isentropique traduit la variation de volume d’un corps lorsque la pression est modifiée, à entropie constante. Ce qui permet d’écrire finalement la relation suivante entre la variation de la masse volumique du fluide et la surpression.

$\mu (x,t)={\mu }_a{\chi }_{s}p(x,t)$

En appliquant le principe fondamental de la dynamique à une tranche de fluide, soumise à une surpression p, nous obtenons :

${\mu }_a\genfrac{}{}{0.1ex}{}{\partial v(x,t)}{\partial t}=-\genfrac{}{}{0.1ex}{}{\partial p(x,t)}{\partial x}$

Et en utilisant le principe de conservation de la masse, on arrive à l’équation vérifiée par la vitesse, sous la forme classique d’une équation de d’Alembert :

$\genfrac{}{}{0.1ex}{}{{\partial }^{2}v(x,t)}{\partial x^2}-\genfrac{}{}{0.1ex}{}{1}{c^2}\genfrac{}{}{0.1ex}{}{{\partial }^{2}v(x,t)}{\partial t^2}=0$

Avec $c=\genfrac{}{}{0.1ex}{}{1}{\sqrt{{\mu }_a{\chi }_s}}$

On observe une compétition entre le terme d’inertie μ_a et le terme d’élasticité χ_s.

Si on assimile l’air à un gaz parfait diatomique, alors le coefficient de compressibilité isentropique vaut :

${\chi }_s=\genfrac{}{}{0.1ex}{}{1}{\gamma P_a}$

Où $\gamma$ est le rapport des capacités calorifiques à pression et volume constants. $\gamma$= 7/5 pour l’air.

En utilisant l'équation d'état du gaz parfait, la vitesse du son dans l'air devient :

$c=\sqrt{\genfrac{}{}{0.1ex}{}{\gamma P_a}{{\mu }_a}}=\sqrt{\genfrac{}{}{0.1ex}{}{\gamma R{T}_a}{M_{air}}}$

Où T_a est la température d'équilibre de l'air et M_air, sa masse molaire, égale à 29 g.mol^-1.

L’application numérique donne, à 20°C, une vitesse de 343 m.s^-1.

La réponse de l’oreille à un stimulus de pression ne suit pas une loi linéaire. En effet, les tests d’écoute montrent que la sensation subjective du volume d’un son est reliée au logarithme de l’excitation physique. Ainsi, on définit le niveau de pression en décibels (dB) par, où p_eff  désigne la valeur efficace de la surpression :

$P_{dB}=20log\genfrac{}{}{0.1ex}{}{p_{eff}}{p_0}$

p₀ , appelée pression de référence, représente la surpression minimale correspondant au seuil d’audition pour une fréquence de 1 000 Hz, p₀= 2.10^-5 Pa. Cette surpression est environ 10¹⁰ fois plus faible que la pression atmosphérique, et représente une amplitude des vibrations du tympan de l’ordre de grandeur du rayon de l’atome d’hydrogène, soit autour de 30 picomètres.

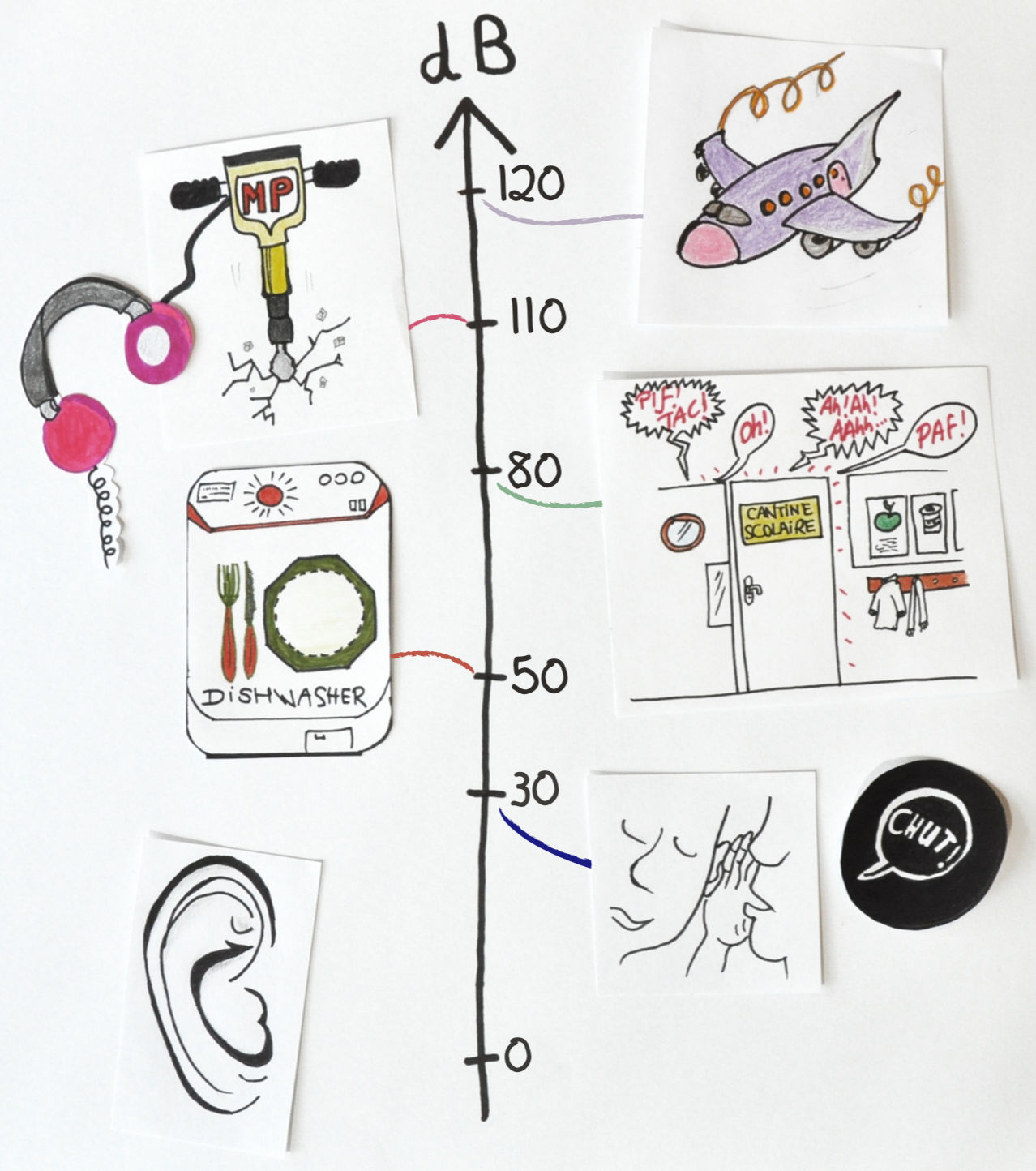
Le son le plus fort supportable par l’oreille correspond à une pression d’environ 20 Pa. On note qu'il y a un rapport de 1 million entre le seuil d’audition et le seuil de douleur de l’oreille. L’utilisation du décibel permet alors de représenter l’étendue des sons audibles sur une échelle de 0 à 120, figure 4.

Donnons quelques ordres de grandeurs :

Figure 4. Échelle des décibels

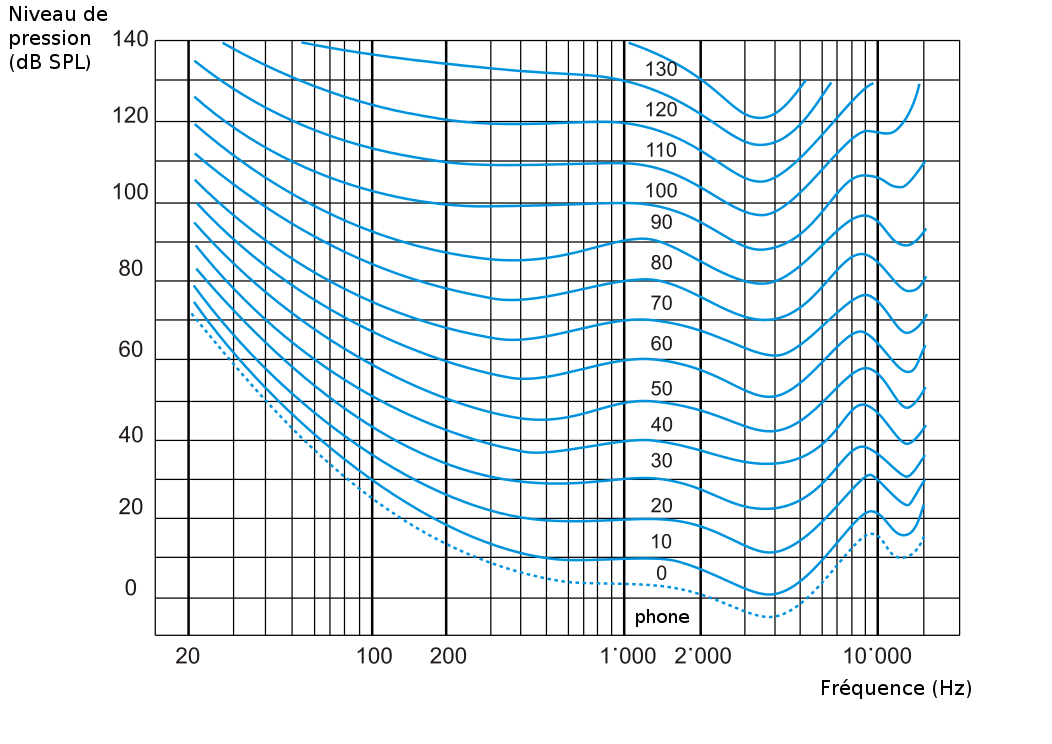
La sensation de volume sonore perçue par l’oreille dépend aussi de la fréquence.

Ce phénomène est présenté par les courbes d’isosonie, figure 5. Les courbes représentent la même perception de volume sonore pour une fréquence donnée. Le test est réalisé en faisant écouter à un groupe de personnes un son sinusoïdal soutenu dont on va faire varier la fréquence et l’amplitude. Chaque courbe représente un même niveau de sensation de volume sonore.

Source - © 2015 Source :Wikimedia

Figure 5. Courbes d'isosonie

Les courbes du haut montrent une allure peu modifiée pour une grande gamme de fréquences. Pour des sons très forts, le niveau d’intensité pour produire la même sensation de volume sonore, ne varie pas beaucoup avec la fréquence. Par contre pour des sons très faibles, la sensation de volume sonore en fonction de la fréquence varie considérablement.

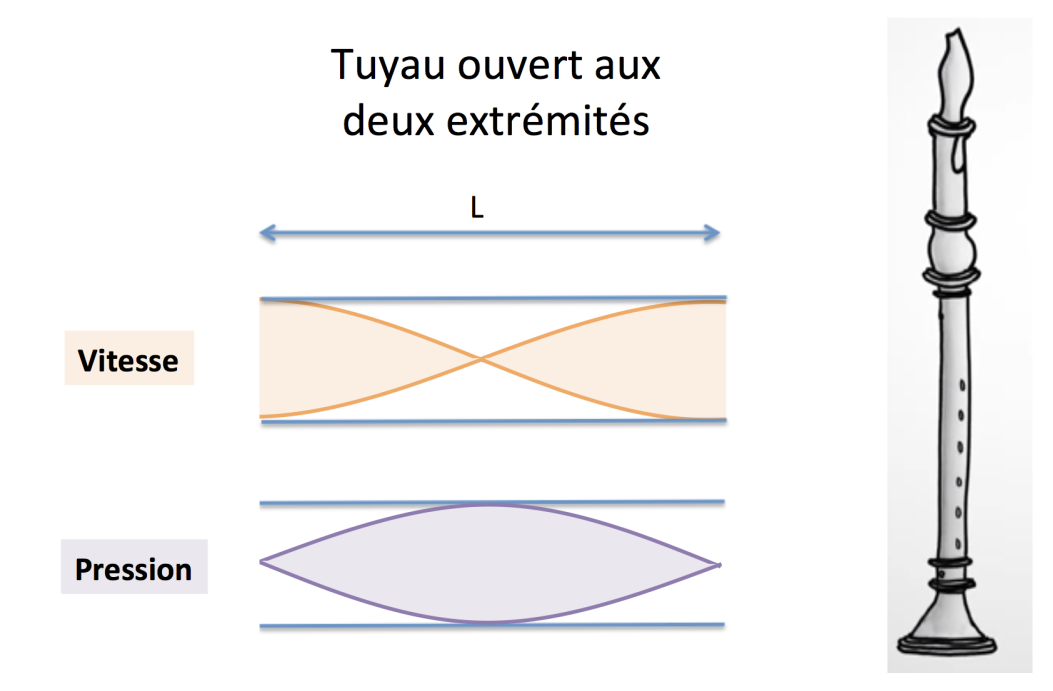
La flûte peut être modélisée comme un tuyau dont les deux extrémités sont ouvertes. L’embouchure est un ventre de vitesse. Le tuyau est ouvert à l’autre extrémité, la surpression y sera alors nulle : on observera un nœud de pression associé à un ventre de vitesse, figure 6.

Figure 6. Modélisation du mode fondamental d'une flûte de longueur L. L'embouchure et le pavillon sont des ventres de vitesse

La longueur d’onde du son fondamental émis par une flûte de longueur L est, lorsque tous les trous sont bouchés, égale à 2 fois L.

Pour une flûte soprano de longueur L = 32,5 cm et en prenant la vitesse du son égale à 340 m.s^-1, on trouve une fréquence du fondamental :

${\nu }_1=\genfrac{}{}{0.1ex}{}{c}{{\lambda }_1}=\genfrac{}{}{0.1ex}{}{c}{2L}=$ 523 Hz.

Cette fréquence correspond au do4.

Remarque : Dans un tuyau ouvert, le nœud de pression n’est en fait pas exactement situé dans le plan terminal du tuyau mais un peu au-delà, à une distance proportionnelle au diamètre du tuyau. La longueur acoustique est plus grande que la longueur géométrique de la flûte.

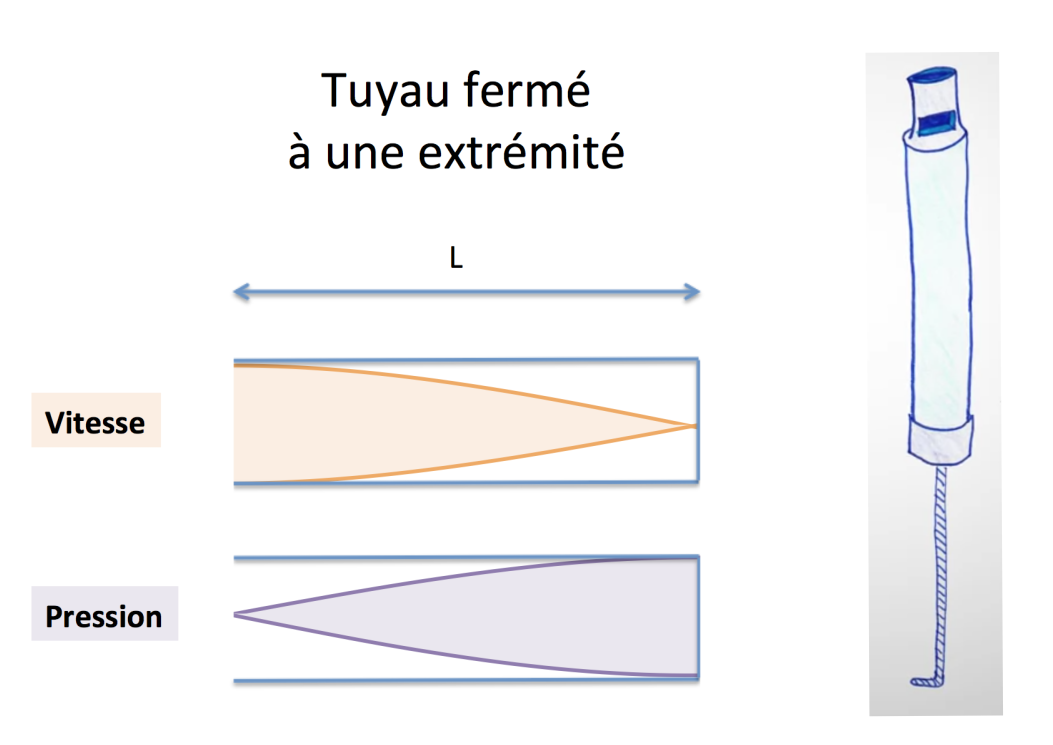
Le jazzoflûte, ou flûte à coulisse peut être modélisé comme un tuyau dont une extrémité est ouverte (l'embouchure) et l’autre est fermée et amovible par un piston. Dans ce cas, à l'extrémité fermée, la vitesse des tranches d’air est nulle et on observe un nœud de vitesse et un ventre de pression, figure 7.

Figure 7. Modélisation du mode fondamental d'un jazzoflûte de longueur L. L'embouchure est un ventre de vitesse, le piston est un nœud de vitesse

La longueur d’onde du son fondamental émis par un jazzoflute de longueur L de 25,5 cm est égale à 4 fois L. La fréquence est alors environ 330 Hz.

Lorsqu’on tire sur le piston, on augmente la colonne d’air et la fréquence diminue.