Le Soleil et ses neutrinos

On peut faire quelques hypothèses : Si le Soleil puisait son énergie du charbon, il serait épuisé en 2000 ans !! Cet ordre de grandeur est valable pour tout scénario dans lequel on veut faire provenir l'énergie du soleil de réactions chimiques : les énergies de liaisons mises en jeu lors de réactions chimiques sont trop faibles pour rendre un tel scénario plausible. Peut-être le Soleil puise-t'il son énergie de la contraction gravitationnelle? Ce scénario fut envisagé vers 1850 par Helmholtz. Lorsque le Soleil se contracte, son énergie potentielle gravitationnelle varie, et cette variation d'énergie potentielle pourrait être transformée en énergie cinétique d'agitation thermique... Calculons, à flux d'énergie émise supposé constant, un ordre de grandeur de la durée de vie du Soleil. Un ordre de grandeur de la variation d'énergie potentielle de pesanteur du Soleil (par exemple, estimons le temps qu'il lui aurait fallu pour passer d'une taille égale à celle de l'orbite terrestre à sa taille actuelle) est G M²/R, si on divise cela par le flux d'énergie que le soleil émet chaque seconde, on obtient une estimation grossière de la durée de vie du Soleil de moins de 30 millions d'années... Ce qui est trop peu étant donné l'âge estimé de la Terre à l'époque de Helmoltz... Depuis Einstein nous savons qu'il y a équivalence masse-énergie par l'intermédiaire de la formule E = m c² Dès lors sachant que la masse du Soleil est grande appliquons cette équivalence pour trouver l'énergie correspondant à la masse entière du soleil : on trouve qu'elle est de l'ordre de 2 × 10⁴⁷J... Si on divise par l'énergie émise à chaque instant, on trouve une durée de vie du Soleil de l'ordre de 10¹⁴ ans... Ceci est plus long que l'âge de l'Univers ! En fait, à chaque réaction, seule une fraction de la masse au repos est libérée sous forme d'énergie, cette fraction est 0,0007 fois la masse au repos du soleil, ce qui correspond à un ordre de grandeur de 1044 J. Ceci nous donne la durée de vie probable du Soleil : 10¹⁰ ans... Le Soleil a donc vécu la moitié de sa vie...

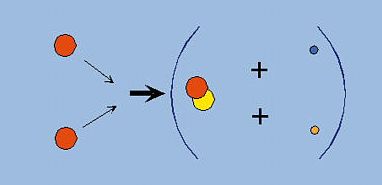
Le Soleil se comporte comme un réacteur à fusion : le confinement est assuré par l'attraction gravitationnelle. La force de gravité est équilibrée par la pression du gaz et l'élévation de température, elle-même entretenue par les réactions nucléaires : 4 protons (noyaux d'Hydrogène) réagissent pour donner une molécule d'Hélium 4 et de l'énergie. 600 millions de tonnes d'hydrogène sont brûlées chaque seconde... les étapes de cette réaction nucléaire sont illustrées ci-dessous : la collision entre deux protons donne du deutéron (noyau de deutérium), un positron (anti-électron) et un neutrino (image 1) : ₁H + ₁H → ₂D + e⁺ + ν

Figure 1. Collision entre deux protons

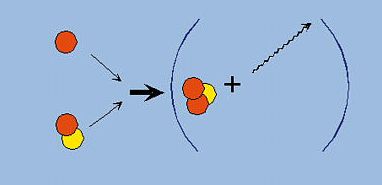
Par la suite, la collision entre le deutéron et un proton donne de l'hélium 3 et un photon (image 2) : ₁H + ₂D → ₃He + γ

Figure 2. Collision entre le deutéron et un proton

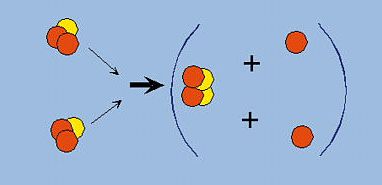
Enfin, deux noyaux d'hélium 3 se combinent pour donner de l'hélium 4 ainsi que deux protons (image 3) : ₃He + ₃He → ₄He + ₁H + ₁H + γ

Figure 3. Combinaison de deux noyaux d'hélium 3

« Remarque : en fait, cette série de réactions est une représentation simplifiée de la réalité. D'autres réactions de fusion existent, quoiqu'elles soient minoritaires. Ces réactions, au lieu d'aboutir à la création de noyaux d'Hélium 4 (aussi appelées particules α), donnent naissance à du Lithium et à du Bore, ainsi qu'à quelques neutrinos supplémentaires. »

Comment obtient-on le chiffre indiqué plus haut : seule 0,0007 fois la masse au repos du Soleil est convertie en énergie via les processus de fusion nucléaire ? Tout d'abord, la fusion nucléaire nécessite une température minimale pour se produire. La température de surface du Soleil est très insuffisante pour provoquer des réactions nucléaires : en fait, les réactions de fusion ont lieu au coeur du Soleil, à 15 millions de degrés, et seule 10% de la masse du Soleil est susceptible d'être brûlée au cours de réactions de fusion nucléaire. Ensuite, lors des réactions de fusion, toute la masse n'est pas convertie en énergie : les hydrogène ne sont pas désintégrés purement et simplement, mais transformés en hélium 4. La diminution de masse correspondant à une réaction de fusion de 4 noyaux d'hydrogène pour donner un noyau d'hélium 4 représente seulement 0,7% de la masse mise en jeu, d'où le facteur multiplicatif 0,1 (10%) × 0,007 (0,7%) = 0,0007 fois la masse totale du Soleil transformée en énergie. Les réactions de fusion au coeur du Soleil laissent échapper (outre l'énergie thermique qu'elles produisent) :

Pour chaque réaction de fusion sont libérés deux neutrinos solaires, et une énergie Q = 0,007 × 4 m_H c² = 4 × 10^-12 J, donc le nombre N de ces réactions est 4 × 10²⁶(énergie produite chaque seconde par le Soleil)/ 4 × 10^-12 ≃ 10³⁸ réactions par seconde. Le nombre de neutrinos qui arrivent sur Terre est par conséquent de 64 milliards par seconde sur une surface équivalente à celle d'un ongle !! (Les neutrinos sont émis dans une sphère de surface 4 π D_Terre-Soleil².) Le flux de neutrinos est 6,4 × 10¹⁰ cm^-2 s^-1

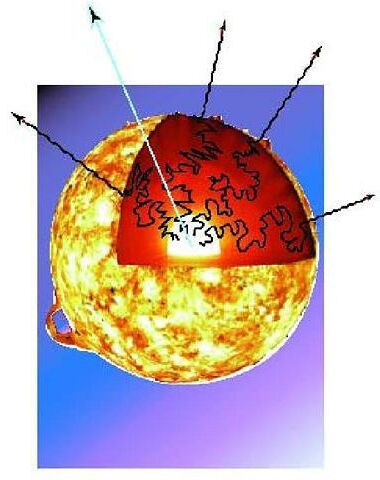
Depuis le centre du Soleil, un neutrino nous arrive en 8 minutes, tandis qu'un photon nous parvient en 1 million d'années... Pourquoi, alors que les deux particules (photon et neutrino se déplacent toutes deux à la vitesse de la lumière dans le vide)? Comme illustré dans la figure ci-dessous, un neutrino (flèche bleue) n'interagit quasiment pas avec son environnement : en se déplaçant à la vitesse de la lumière, il lui faut 8 minutes pour arriver sur Terre. Un photon, à titre de comparaison, va interagir un nombre incalculable de fois à l'intérieur du Soleil avant de parvenir à sa surface : si le photon met lui aussi 8 minutes à nous parvenir depuis la surface du Soleil, il lui faut en revanche un million d'années ou plus pour parcourir le trajet qui le mène du coeur à la surface.

Figure 4. Comparaison des temps de parcours d'un neutrino et d'un photon du centre du Soleil vers la Terre : 8 minutes contre plus d'un millions d'années

Cette quasi-absence d'interaction des neutrinos avec la matière fait que la majeure partie des neutrinos traversent la Terre "sans la voir"... Il est donc a fortiori très difficile de détecter les neutrinos... Un certain nombre de détecteurs existent cependant à travers le monde : aux Etats-Unis (en particulier au Dakota), à Baksan dans le Caucase, en Italie (Laboratoire National du Gran-Sasso), au Japon (détecteur Kamiokande) et au Canada (Ontario). Citons enfin le détecteur français de matière noire au laboratoire souterrain de Modane.

On ne trouve pas le nombre de neutrinos auquel on s'attendait ! Les différents détecteurs donnent une estimation grossière du déficit en neutrinos : la moitié peut-être seulement des neutrinos solaires prédits par la théorie sont détectés !

Explication(s) ?

Le déficit des neutrinos solaires fut à l'origine d'un débat très animé pendant plus de 30 ans. Les flux de neutrinos issus du Soleil dépendent fortement de la température et par conséquent pourraient être sensibles aux incertitudes sur la modélisation du Soleil. D'autre part si le neutrino a une masse, d'après la théorie il pourrait changer de nature et par suite être indétectable. Ces deux réponses possibles parmi les plus probables ont agité la communauté scientifique et donné naissance à des expériences difficiles pour détecter avec précision les neutrinos issus du Soleil. Ces expériences qui ont vu le jour dans les années 1970 ont abouti dans les années 2000 a la conclusion que le neutrino changeait de nature sur sa trajectoire - on dit que le neutrino oscille - et que le flux calculé du soleil était parfaitement exact.