Activer le mode zen
Ressource au format PDF
Mots-clés
- LASER
- MASER
- onde radio
- émission induite
- émission stimulée
- émission spontanée
- inversion de population
- photon
Classification
Laser et maser
17/02/2011
Résumé
Un article du dossier « Les lasers en questions ». Pourquoi le MASER fut-il réalisé avant le LASER ?
Charles Townes réalisa le premier maser à ammoniac en 1954 et Ted Maiman le premier laser à rubis en 1960.
Comment expliquer que le premier MASER (Microwaves Amplification by Stimulated Emission of Radiation) fut réalisé avant le premier LASER (Light Amplification by Stimulated Emission of Radiation) ?
Le maser et le laser fonctionnent sur le même principe d'amplification du rayonnement basé sur l'émission stimulée (appelée souvent induite). Le maser émet un rayonnement dans le domaine radio à des longueurs d'onde très supérieures (du millimètre au mètre) à celles des lasers qui fonctionnent en optique dans le domaine visible (λ ≈ 400-700 nm) ou infra-rouge (λ ≈ 1-10 μm).
L'émission de photons est produite par des transitions d'une particule (atome ou molécule) qui passe d'un état haut 2 vers un état bas 1. Contrairement à l'émission spontanée isotrope, l'émission stimulée (ou induite ce qui est synonyme) émet un photon qui se propage strictement dans la même direction que le photon « stimulant » (figure 1 ci-dessous). C'est ce qui conduit aux propriétés du faisceau : directivité et cohérence.
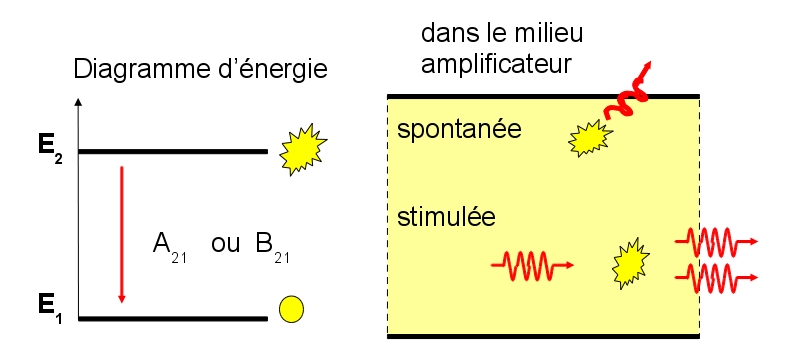
Usuellement, l’émission spontanée est prépondérante ; dans un laser ou un maser, l’émission stimulée l’emporte.
Quand on a réalisé une surpopulation suffisante de l'état haut (inversion de population) l'amplification maser, ou laser, peut se déclencher à condition que l'émission stimulée l'emporte sur l'émission spontanée.
Les probabilités d'émission spontanée et stimulée sont proportionnelles aux coefficients d'Einstein A21 et B21 liés par la relation suivante : B21 / A21 = λ3 / 8 π h. La définition précise et les ordres de grandeur des quantités A21 et B21 sont détaillées dans la note ci-dessous.
On voit que ce rapport varie fortement en fonction de la longueur d'onde. Dans le domaine radio, l'importance relative de l'émission stimulée, de coefficient B21, par rapport à l'émission spontanée, de coefficient A21, est beaucoup plus grande que dans le domaine optique.
Or l'émission spontanée représente un handicap pour l'amplification laser : les photons correspondants se dispersent dans toutes les directions, tandis que les photons dus à l'émission stimulée se concentrent dans le faisceau directif du laser.
C'est ce qui explique que c'est d'abord un MASER à ammoniac qui a pu être réalisé en 1954 par Townes, Gordon et Zeiger, à l'université Columbia de New York.
Charles Townes a ensuite « stimulé » la suite des recherches pour obtenir le LASER, c'est-à-dire le même effet dans le domaine optique. C'est en 1960 qu'un premier laser à rubis émettant dans le rouge à la longueur d'onde 694,3 nm fut réalisé par Theodore Maiman. Le jeune Maiman (32 ans) travaillait dans un laboratoire industriel de Californie, le « Hughes Research Laboratories », à Malibu.
À voir ou revoir sur CultureSciences-Physique : « Pré-histoire et histoire du LASER », une conférence de Bernard Cagnac qui retrace l'histoire de la découverte du laser.
Les nombres de transitions relatives à l'émission spontanée et stimulée sont :
Nspontanée = n2 A21 (1)
Ninduite = n2 B21 Uν (2)
où Ns et Ni sont les nombres de transitions spontanées et induites par unité de temps et par unité de volume du milieu. Ils sont proportionnels au nombre n2 de particules excitées dans l'état 2 par unité de volume. L'émission stimulée est en outre proportionnelle à Uν, densité du rayonnement « stimulant » dont la fréquence ν est accordée à celle de la transition (E2 -E1 = h ν).
Les coefficients A21 et B21 sont deux caractéristiques de la transition considérée, appelés coefficients d'Einstein.
C'est en effet Einstein qui fut le premier à prévoir et décrire le phénomène d'émission stimulée en 1917, posant ainsi le principe du fonctionnement d'un laser.
Le coefficient A21 représente la probabilité d'émission spontanée par unité de temps. En unité de s-1, l'ordre de grandeur est de 109 pour une raie atomique forte et 104 pour une raie très faible. Notons que les lasers fonctionnent sur des raies à faible probabilité de transition, condition favorable pour réaliser l'inversion de population.
N.B. : La relation qui lie les coefficients d'Einstein découle d’un principe général de la physique statistique, le principe des « bilans détaillés », selon lequel un équilibre thermodynamique est réalisé si il y a une compensation exacte des processus microscopiques directs et inverses.
Dans le cas des interactions entre atomes (ou molécules) et photons, on doit compter aussi le mécanisme d'absorption, avec le coefficient d'Einstein correspondant B12 = g2/g1 B21 où g2/g1 est le rapport des poids statistiques des deux états quantiques de la transition.
Remarque sur les unités :
Le coefficient B21 (ou B12) n'a pas la même dimension que le coefficient A21. Sa définition et son unité dépendent de la grandeur choisie comme intensité du rayonnement qui induit soit des désexcitations 2-->1 par émission stimulée soit des excitations 1-->2 par absorption.
Ici nous avons choisi la grandeur Uν, définie comme l'énergie du rayonnement présent dans l'unité de volume par unité d'intervalle spectral en fréquence. On vérifie alors que le rapport A21/B21 de même que Uν est homogène à une énergie divisée par une longueur à la puissance 3 et par une fréquence.
Pour citer cet article :
Laser et maser, Marie-Christine Artru, février 2011. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/laser-maser.xml




