Laser et indice de l'air

Pourquoi les applications du laser nécessitent-elles de connaître l'indice de réfraction de l'air atmosphérique avec une très grande précision ?

La connaissance précise de l’indice de l’air est importante pour différentes applications du laser. D’une part la présence de l'air affecte les mesures de longueurs d'onde en laboratoire qui exploitent la finesse spectrale des raies laser (voir par exemple la définition du mètre). D’autre part, les mesures de télémétrie sont fondées sur le temps de trajet d’un faisceau laser et doivent tenir compte de la propagation dans l’air : l’effet de la traversée de l’atmosphère terrestre ajoute environ 0,3 μs, délai variable selon son humidité (voir les mesures du laser terre-lune).

La longueur d'onde λ_air, usuelle en spectroscopie, est celle de la radiation lumineuse se propageant dans l'air, mesurée au sol dans les conditions atmosphériques normales. La valeur de λ_air est différente de la longueur d'onde λ_vide que l'on déduit de l'énergie du photon h ν par :

λ_vide = c₀/ ν = 1/ σ où c₀ est la vitesse de la lumière dans le vide.

C'est la fréquence ν qui est conservée quand la lumière passe du vide à un milieu transparent « réfringent », mais la vitesse de propagation et la longueur d’onde sont modifiées. L'indice de réfraction n dépend des caractéristiques diélectriques (permittivité ε_r et susceptibilité χ) des constituants du milieu, molécules du gaz ou atomes du cristal. La relation n² = ε_r = 1 + χ traduit le fait que le champ électrique de l’onde lumineuse déforme les cortèges d’électrons liés et que la polarisation induite agit en retour sur la propagation de l’onde.

L'indice de l'air n qui nous entoure est égale à environ 1,0003. Dans l'air la vitesse de la lumière est c_air = c₀ / n et la longueur d'onde devient λ_air = c_air / ν = λ_vide / n.

Ce qui conduit à la différence : λ_vide – λ_air = λ_vide x (n-1) / n.

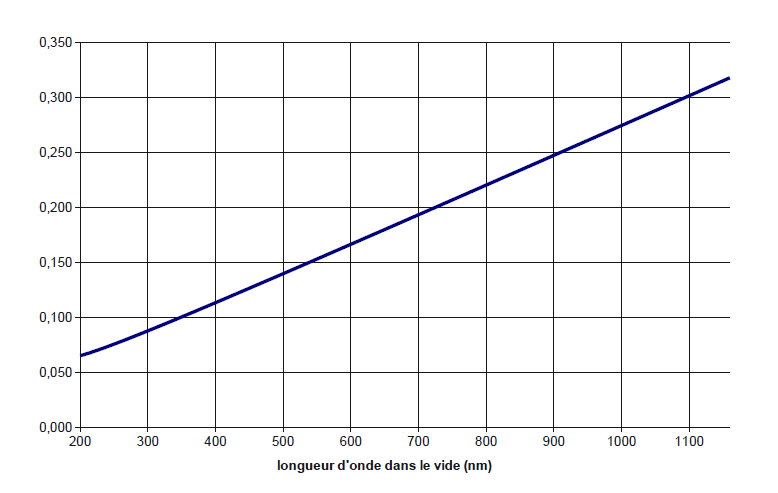
La figure montre la variation de la correction λ_vide – λ_air pour la lumière, de l’ultra-violet à l’infra-rouge.

La différence de l'ordre de 3 . 10^-4 en valeur relative est significative en spectroscopie où les mesures de longueurs d'onde sont couramment réalisées avec des précisions de 10^-6. Par exemple, un spectrographe usuel utilisant un réseau échelle avec 500 traits/mm, large de 50 mm, et utilisé dans l'ordre 40 permet une résolution spectrale R = λ / Δλ = 50 x 500 x 40 = 10⁶.

Avec des lasers monomodes et les méthodes interférométriques, les ordres de grandeurs des précisions nécessaires et atteintes dépassent 10^-15. Pour les précisions extrêmes, notamment en métrologie, les expériences doivent être réalisées sous vide pour mesurer directement λ_vide.

Actuellement des équations très complètes sont élaborées pour modéliser précisément l'indice de l'air en fonction de la pression et de la température, en tenant compte des composants minoritaires (présence de CO₂, humidité) ainsi que de la dépendance en longueur d'onde (effet faiblement « dispersif »).

Les résultats les plus précis (jusqu'à 10^-8) sont mis à jour au National Institute of Standards and Technology et accessibles sur le lien http://emtoolbox.nist.gov/Wavelength/Documentation.asp.

La courbe donnée ici est basée sur un article de 1966 qui sert encore de standard pour la conversion des valeurs de λ_air mesurées en laboratoire. Nous en reproduisons ci-dessous l'abstract.

La valeur représentée en ordonnée est 10³ (λ_vide - λ_air).

Figure 1. Différence entre les longueurs d'onde dans le vide et dans l'air dans les conditions atmosphériques normales

B Edlén - 1966 - Metrologia 2,71 - ABSTRACT

« Present knowledge of the refractive index of air is reviewed. Regarding the absolute values there are as yet no definite indications that the standard adopted in 1953 on the basis of Barrell and Sears' measurements should be changed, but new experiments aiming at reducing the present uncertainty of about ± 5 x 10^-8 would be desirable.

Several recent investigations have contributed important new information on the dispersion of air, which has made it possible to derive an improved dispersion formula for standard air, (n - 1)_s x 10⁸ = 8342.13 + 2406030 (130 - σ²)^-1 + 15997 (38.9 - σ²)⁻¹, where σ is the vacuum wave-number in μm^-1. The deviations from the 1953 formula are small and practically negligible in most spectroscopic work.

An equation for the dependence of refractivity on temperature and pressure based on theoretical considerations has been derived. For the range of atmospheric conditions normally found in a laboratory the equation can be approximated by the formula (n - 1)_tp = (n - 1)_s x 0.00138823 p/(1 + 0.003671 t), with p in torr, t in °C, and (n - 1)_s given by the dispersion formula for standard air.

The effect of carbon dioxide and water vapour is discussed. From Erickson's dispersion data for water vapour, combined with Barrell and Sears' absolute measurements, one obtains the equation n_tpf - n_tp = −f (5.722 - 0.0457 σ²) x 10^-8 for the difference in refractive index of moist air, containing f torr of water vapour, and dry air at equal temperature and total pressure. The equation is valid for visible radiations and normal atmospheric conditions. »