Activer le mode zen
Ressource au format PDF
Mots-clés
- LASER
- ultraviolet
- conversion de fréquence
- fréquence
- cristal
- milieu diélectrique
Classification
Laser dans l'ultra-violet
24/02/2011
Résumé
Un article du dossier « Les lasers en questions ». Comment réalise-t-on des lasers émettant dans l'ultra-violet ?
Quelles sont les difficultés rencontrées pour réaliser des lasers dans le domaine de l'ultra-violet sur le même principe que celui des lasers usuels qui émettent des radiations visibles ou infra-rouges ? Par quel moyen réalise-t-on des sources de rayonnement ultra-violet possédant les mêmes propriétés que les lasers ?
La réalisation d'un laser émettant un rayonnement ultra-violet (note 1) se heurte à deux difficultés. La première est la tendance défavorable du rapport entre les probabilités d'émission stimulée B21 et spontanée A21. Ce rapport, proportionnel à λ3 (voir les détails dans l'article « Laser et maser »), diminue fortement vers les courtes longueurs d'onde.
La deuxième difficulté est d'ordre technique. Tous les verres ou quartz sont opaques aux longueurs d'ondes inférieures à environ 100 nm. On ne peut donc pas réaliser de cavité laser contenant le milieu actif, gazeux ou liquide, faute de « fenêtre » permettant au rayonnement de sortir à l'extrémité de la cavité.
Pour obtenir un faisceau laser en UV lointain, on réalise une « conversion de fréquence » à partir d'un laser émettant de la lumière visible ou infra-rouge. En multipliant par 2 la fréquence ν émise par le laser, on divise par 2 la longueur d'onde λ = c / ν, ce qui permet d’atteindre l’ultra-violet par étape.
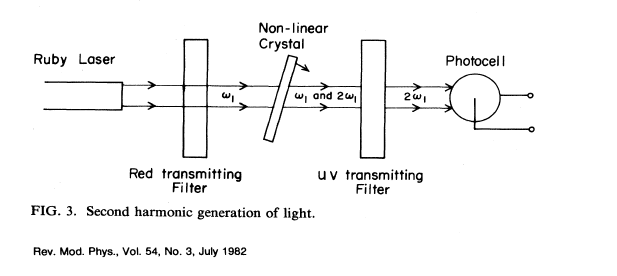
Une des premières expériences de « doublement de fréquence » a été réalisée dès 1961 par Bloembergen (prix Nobel 1981, voir « Lasers et prix Nobel »). Ci-dessous est reproduite la figure d'un de ses articles où il en résume le principe : un faisceau laser, monochromatique de pulsation ω1 = 2 π ν1 (rouge, λ ∼ 600 nm) traverse une lame taillée dans un cristal « non-linéaire ». Au sortir de la lame apparaît une deuxième radiation de fréquence 2ω1 (UV, λ ∼ 300nm) ; le filtre interposé sélectionne la radiation de fréquence 2ω1. La radiation de fréquence 2ω1 correspond au deuxième harmonique d’une radiation de fréquence fondamentale ω1 qui n’est plus parfaitement monochromatique sous l’effet du milieu non-linéaire (note 2).
Pour une onde électromagnétique monochromatique incidente de champ électrique Ei = E0 cos(ωt), l’effet non-linéaire génère dans le cristal une polarisation proportionnelle à (Ei)2 dont un terme varie en cos(2ωt), ce qui produit l’onde de fréquence double.
Un milieu non-linéaire permet aussi de générer une onde de fréquence ν1+ν2 à partir de deux ondes monochromatiques de fréquences ν1 et ν2.
Les techniques de conversion de fréquence sont maintenant entrées dans le domaine industriel et sont largement utilisées dans de nombreuses applications (voir exemple figure ci-dessous).
Des recherches actuelles portent sur l’amélioration des performances et en particulier sur la génération d’harmoniques d'ordre très élevé.
Doubleur automatique de fréquence pour lasers Ti:saphir - Micro Controle Spectra-Physics. « Le doubleur Inspire Blue transforme la lumière IR des lasers Ti:saphir (entre 690 et 1040 nm) en UV proche ou en lumière visible (entre 345 et 520 nm). Basé sur une technologie non linéaire novatrice, il produit un faisceau d’une qualité exceptionnelle, avec un bon rendement (jusqu’à 50 %) et un faible élargissement des impulsions. (...) »
1. L'ultra-violet désigne les radiations de longueurs d'onde inférieures à celles du rayonnement visible.
Dans l'UV proche (λ de 400 à 200 nm), l'ozone de la haute atmosphère terrestre absorbe progressivement les radiations solaires.
Aux longueurs d'onde inférieures à 200 nm, l'air devient opaque, du fait de l'absorption de l'oxygène. Les dispositifs de laboratoires doivent alors fonctionner sous vide et les observations astronomiques s’obtiennent à partir de satellites. Ce domaine de l'ultra-violet « lointain » ( λ de 200 à 10 nm environ) est aussi désigné « extrême UV » ou « UV du vide ».
Aux longueurs d’onde inférieures à 1 nm, l'air redevient transparent, on passe au domaine des rayons X, puis à celui des rayons gamma.
2. Un milieu diélectrique réagit à la présence d’un champ électrique E par un léger déplacement global des nuages électroniques des atomes ou molécules, ce qui produit une densité de polarisation P.
Dans un cristal linéaire, le vecteur polarisation est proportionnel au champ électrique E selon la relation P = χ ε0 E. Rappelons que, pour un milieu isotrope transparent, les vecteurs P et E sont colinéaires et que l’indice n dépend directement du facteur χ (susceptibilité diélectrique) par n2 = 1+χ.
Dans un milieu non-linéaire, le module du vecteur polarisation n’est pas strictement proportionnel au champ électrique. On l’exprime par un développement du type P = ε0 (χE + χ2E2 + χ3E3 + ...).
L’effet « non-linéaire » apparaît pour certaines structures cristallines non centro-symétriques. En effet le terme d’ordre 2 est nul s’il y a un centre de symétrie, car l’inversion de E en -E implique alors l’inversion de P en -P. En particulier les verres en silice doivent être dopés au germanium ou au phosphore pour fournir des milieux non-linéaires.
Les coefficients χ2, χ3, ... sont très petits (χ2 de l'ordre de 10-10 à 10-13 mV-1) de sorte qu’il faut de très grandes valeurs du champ électrique pour que les termes non-linéaires deviennent significatifs par rapport au terme linéaire. Ceci explique qu’on observe et exploite les effets non-linéaires grâce à des faisceaux lasers de très fortes intensités.
Exemple et ordres de grandeur :
Pour le cristal KTP (KTiOPO4, phosphate de titanyle et de potassium) qui est largement employé, on a les valeurs χ = 1,89 et χ2 = 5.10-12 mV-1. Il faut donc un champ électrique élevé de l’ordre de 1010 Vm-1 pour que le premier terme non-linéaire atteigne quelques % du terme linéaire. Traduisons cette valeur en puissance de faisceau laser, sachant que le flux d’énergie F d’un faisceau parallèle s’exprime en fonction de la valeur efficace du champ électrique E par F = c ε0E2. On trouve un flux d’énergie d’environ 3.1017 Wm-2, soit une puissance de 3.1011 W si la section d’impact est de l’ordre du mm2.
Il est possible de produire cette puissance instantanée par un laser pulsé de type YAG, l’énergie étant concentrée dans de très brèves impulsions, par exemple 10 J en 0,1 ns.
Pour citer cet article :
Laser dans l'ultra-violet, Marie-Christine Artru, février 2011. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/laser-UV.xml