Activer le mode zen
Ressource au format PDF
Mots-clés
limite de Roche anneaux de Saturne satellite forces de marées force de marée cohésion d'un satelliteClassification
Anneaux de Saturne et limite de Roche
13/07/2004
Résumé
Un satellite peut-il orbiter à n'importe quelle distance de sa planète ? Quelle est la structure des anneaux de Saturne ? Comprendre ce qu'est la limite de Roche permet de répondre à ces questions.
Table des matières
On sait aujourd'hui que les anneaux de Saturne sont essentiellement composés de particules et objets de faible diamètre, constitués principalement de glace, en orbite autour de la planète.
Toutefois, pendant un certain temps, on a supposé que ces anneaux pouvaient être "d'un seul tenant".
De nos jours, grâce aux travaux de Roche en 1850, on sait que des anneaux solides à cette distance de Saturne seraient impossibles : ils seraient détruits par les forces de marée. Ces mêmes travaux prédisent qu'aucun gros satellite ne peut être en orbite très près de Saturne. Les prédictions de Roche sur les anneaux ont été vérifiées par les diverses sondes qu'on a depuis lors envoyées vers les anneaux (Voyager 1 et 2, et aujourd'hui Cassini-Huygens).
Figure 1. Saturne et ses anneaux
Le but de cette fiche est d'expliquer brièvement et simplement la limite de Roche
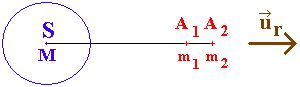
On considère une planète de masse M, supposée sphérique, dont le centre S est situé à la distance R d'une masse m1 et à la distance R + r d'une masse m2, le centre de la planète, m1 et m2 étant supposés alignés.
A1 = position de la masse m1, A2 = position de la masse m2, SA1 = R, A1A2 = r
La masse m1, étant plus proche de la planète que la masse m2, est plus attirée par la planète que cette-dernière.
Par conséquent, la différence entre les forces exercées par la planète sur m1 et m2 a tendance à éloigner les deux masses. Ce phénomène est à l'origine des forces de marée et est analogue à l'influence exercée par la Lune sur les masses fluides (et solides...) de la Terre.
Les deux masses m1 et m2 sont en interaction gravitationnelle. Cette force a tendance à les rapprocher.
La question que l'on se pose est ...
...A partir de quelle distance R0 à la planète est-ce que les forces de marée l'emportent sur les forces gravitationnelles?
Lorsque le système (m1,m2) est à une distance à la planète inférieure à R0, alors les forces qui s'exercent sur lui vont éloigner m1 et m2, et donc dissocier le système.
Accélération de m1 dans le référentiel galiléen centré sur la planète centrale :
a1 = (- G M/R2 + G m2/r2) ur |
Accélération de m2 dans le même référentiel :
a2 = (- G M/(R+r)2 + G m1/r2) ur |
d'où
d2A1A2/dt2 = a2 - a1 = - G [-M (1/R2 - 1/(R+r)2) + (m1 + m2)/r2] ur |
Le terme -G (m1 + m2)/r2ur, de sens opposé à celui de A1A2, traduit l'attraction gravitationnelle entre les deux masses, qui tend à faire diminuer la distance A1A2, tandis que le terme G M (1/R2 - 1/(R+r)2) ur, de même sens que A1A2, traduit les forces de marée qui tendent à séparer A1 de A2.
Les forces de marée l'emportent sur l'attraction gravitationnelle entre les deux masses si :
(m1 + m2)/r2 < M (1/R2 - 1/(R+r)2) |
Si m1 + m2 = m est la masse du système et r ≪ R, on a
m/r2 < M/R2 (1 - (1+r/R)-2) ≃ 2 M/R3 r
soit
m/r3 < 2 M/R3 |
m = m1 + m2, masse totale du système
Si on considère notre système comme un modèle simplifié de satellite de diamètre r, m/r3 donne un ordre de grandeur de la masse volumique ρ de ce satellite, donc, en ordre de grandeur, la distance minimale R0 à laquelle ce satellite peut de trouver sans être détruit par les forces de marée causées par la planète de masse M est :
R0 de l'ordre de (M/ρ)1/3 |
Comme, dans ce calcul, on a considéré un satellite constitué de deux masses ponctuelles, et que de plus l'on a considéré que la cohésion du satellite était assurée exclusivement par les interactions gravitationnelles, cette valeur n'est qu'un ordre de grandeur. Un calcul avec un satellite sphérique sans force de cohésion interne donne la valeur approchée :
R0 ≃ (3,5 M/ρ)1/3 |
et la prise en compte des forces de cohésion internes (variables suivant la nature du satellite) modifie encore ce résultat. Cette valeur, cependant, permet de comprendre l'existence d'anneaux de "poussières" à proximité de Saturne : ces poussières n'ont pu s'aggréger sous l'effet des forces gravitationnelles pour devenir un satellite, à l'inverse, les éventuels satellites de grande taille situés dans cette zone sont désagrégés en poussière.
 Figure 3. Saturne et son satellite Titan |  Figure 4. Les anneaux de Saturne |
Application :
Soit un objet de même masse volumique que celle de Saturne (ρ = 6,9 × 105 kg/m3), en orbite autour de Saturne (MSaturne = 5,7 × 1026 kg); sa limite de Roche est, en appliquant la formule précédente : R0≃ 1,4 × 107 m
Pour citer cet article :
Anneaux de Saturne et limite de Roche, Gabrielle Bonnet, juillet 2004. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Roche.xml
