Activer le mode zen
Ressource au format PDF
Mots-clés
- délocalisation
- dualité onde-corpuscule
- chat de Schrödinger
- Feynmam
Classification
Fenêtre ouverte sur la physique quantique
21/10/2004
Résumé
Présentation, en termes simples et avec le moins de mathématiques et de prérequis possibles, des idées principales de la physique quantique : délocalisation des particules, dualité onde-corpuscule, relations d'incertitude, indiscernabilité, et "paradoxes" de la physique quantique. Introduction à la méthode des intégrales de Feynmam.
Table des matières
- Onde ou corpuscule
- Représentation classique de l'électron : la notion de corpuscule
- Représentation de la lumière dans l'électromagnétisme de Maxwell : la notion d'onde
- La physique quantique introduit une autre notion sans analogie dans notre vie quotidienne
- Les relations d'incertitude
- Indiscernabilité
- Paradoxe ? Le chat de Schrödinger
- Les intégrales de Feynman
- Conclusion
- Testez-vous !
Onde ou corpuscule
Représentation classique de l'électron : la notion de corpuscule
Classiquement, l'électron est représenté par un corpuscule. Un corpuscule est assimilable à une toute petite bille : suivant cette représentation, les électrons autour du noyau des atomes se comportent comme des satellites autour d'une planète, et les électrons isolés ont un comportement analogue, toutes proportions gardées, à celui d'une sphère à notre échelle : un ballon de football, une boule de billard...
L'analogie utilisée par Feynman pour expliquer le comportement, suivant la représentation classique -on va voir au 1.3. en quoi cette représentation est inadaptée-, d'électrons lancés par un canon à électrons sur un détecteur, est celle de balles de fusil.
Supposons que l'on tire des balles de fusil de façon aléatoire, avec une dispersion très large, sur une plaque épaisse percée de deux trous, suivie d'un détecteur. On suppose aussi que, lorsqu'elles passent par un trou, les balles sont déviées de façon aléatoire, ce qui fait qu'elles arrivent sur le détecteur avec une certaine dispersion autour du prolongement de la ligne fusil-trou.
On peut fermer un trou, et regarder les balles qui arrivent sur le détecteur :

Figure 1.
Si on ferme l'autre trou, on obtient une courbe similaire, qui est simplement décalée par rapport à la première :
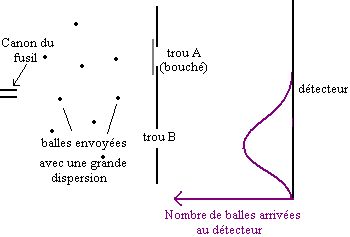
Figure 2.
Si les deux trous sont ouverts, le nombre d'impacts de balle reçus sur le détecteur est la somme des impacts de balles passées par le trou A, donnés par la courbe 1, et de ceux des balles passées par le trou B, donnés par la courbe 2.
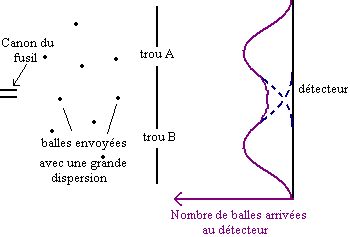
Figure 3.
Le résultat de cette expérience se déduit donc aisément de la connaissance des courbes 1 et 2.
Représentation de la lumière dans l'électromagnétisme de Maxwell : la notion d'onde
Dans l'électromagnétisme de Maxwell, la lumière se comporte comme une onde tridimensionnelle. Cette onde, qui peut se propager dans le vide, sans support matériel, est généralement plus difficile à appréhender que les ondes que l'on peut observer à la surface d'un plan d'eau, toutefois, bon nombre de ses comportements peuvent se comprendre à l'aide de cette analogie.
Lorsqu'une onde sphérique se propageant à la surface de l'eau rencontre une plaque percée de deux trous (semblable au dispositif du 1.), au-delà de la plaque, deux ondelettes sphériques se propagent à partir des deux orifices et interfèrent entre elles.
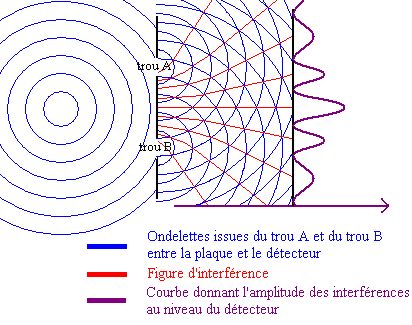
Figure 4.
L'intensité de la perturbation perçue au niveau du détecteur lorsque les deux trous sont ouverts n'est pas égale à la somme des intensités détectées lorsque A et B sont ouverts séparément. Il y a interférence.
De la même façon, une onde lumineuse passant à travers deux orifices suivis d'un écran donne une figure d'interférence :
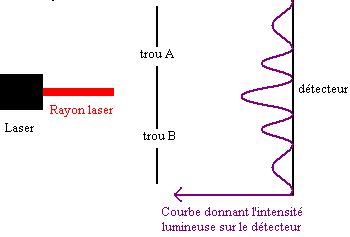
Figure 5.
Cette expérience reproduit, avec des moyens modernes, les résultats de l'expérience dite "des trous d'Young". De ce point de vue là, le comportement d'une onde lumineuse et celui d'une onde à la surface de l'eau sont très proches.
La physique quantique introduit une autre notion sans analogie dans notre vie quotidienne
Lorsque les balles de fusil sont remplacées par des électrons... La "dualité onde-corpuscule"
Effectuons à nouveau, au moins par la pensée, l'expérience que nous avons décrite pour des balles de fusil, mais cette fois-ci avec des électrons. On place donc un canon à électrons, qui envoie des électrons suivant des trajectoires assez dispersées, sur une plaque munie de deux trous, suivie d'un détecteur.
On fait l'expérience lorsqu'un seul trou, le trou A, est ouvert :
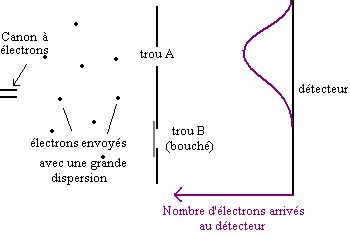
Figure 6.
On fait l'expérience lorsque le trou B seul est ouvert :
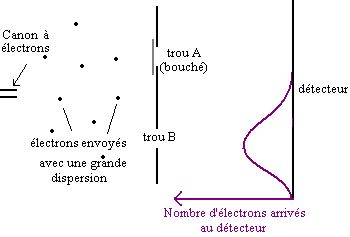
Figure 7.
On fait l'expérience lorsque A et B sont ouverts :
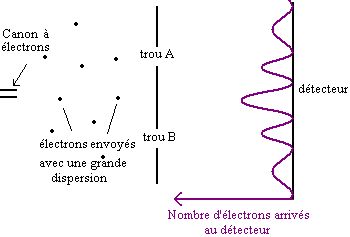
Figure 8.
Classiquement, on représente les électrons comme des corpuscules, mais, lorsqu'on envoie un grand nombre d'électrons sur la plaque, on constate que l'on obtient sur le détecteur une figure d'interférence très semblable à celle que l'on obtient avec une onde.
Les électrons seraient-ils donc une onde ?
On peut faire d'autres expériences pour tester cette hypothèse. Par exemple, on envoie les électrons un par un à travers la plaque. A chaque impact sur le détecteur, on reçoit un "bip" localisé à un endroit précis du détecteur. Ceci n'est pas le comportement d'une onde, mais d'un corpuscule.
Les électrons sont-ils alors des corpuscules qui, lorsqu'ils sont envoyés en grand nombre sur la plaque, créent une "figure d'interférence" à cause des chocs qui surviennent entre eux ?
Pour tester cette hypothèse, il suffit d'envoyer les électrons un par un, empêchant ainsi tout choc. Lorsqu'on fait l'expérience, on obtient tout d'abord un "bip" localisé, puis un autre, etc... comme on s'y attendrait avec des corpuscules sans interaction mutuelle, cependant, lorsqu'on attend suffisamment longtemps pour avoir un grand nombre d'impacts d'électrons individuels sur le détecteur, on voit la figure d'interférence obtenue précédemment se reconstituer...
Qu'en déduire ?
L'électron quantique n'est pas un corpuscule classique : un corpuscule classique ne pourrait pas créer une telle figure d'interférence... Cependant, ce n'est pas non plus une onde comme celles dont on a l'habitude : avec une onde, on ne peut pas obtenir un "bip" localisé sur le détecteur, ce comportement-là est plutôt caractéristique d'un corpuscule...
On parle de "dualité onde-corpuscule". Ce mot, qui traduit le mélange de comportements ondulatoires et corpusculaires caractéristique de l'électron, cache en fait une notion sans équivalent en physique classique.
Localisation de l'électron
Si un électron n'est, ni vraiment une onde, ni vraiment un corpuscule, qu'est-ce que c'est ?
Les expériences faites jusqu'à présent n'ont pu trouver aucune interprétation "classique" au comportement de l'électron, ou à celui de la lumière (qui -on peut le montrer par des expériences semblables à celles que l'on a évoquées pour les électrons- se comporte elle aussi tantôt comme une "particule" de lumière, le photon, et tantôt comme une onde); comme à celui des protons, des neutrons, ou des quarks... Un électron (ou un photon, etc.) est un type d'objet totalement différent de ceux que l'on perçoit autour de nous dans la vie de tous les jours.
Une façon de comprendre le comportement de l'électron consiste à se le représenter comme un corpuscule (une "toute petite bille") qui est le plus souvent non localisée*.
Qu'est-ce qu'une "bille non localisée" ?
Une petite bille classique sur votre bureau est localisée, elle se trouve à un endroit précis. Une petite bille classique que vous avez perdue de telle sorte que vous ignoriez totalement où elle se trouve est là encore localisée : elle se trouve bien quelque part même si vous ne savez pas où....
Un corpuscule quantique non localisé est très différent : il se comporte comme une petite bille qui se trouverait en plusieurs endroits à la fois : par exemple, surtout sur votre bureau mais aussi un peu par terre!

La "bille délocalisée"... Une idée bien étrange... Mais, si cette idée est irréaliste à notre échelle, elle est pertinente à l'échelle atomique
Figure 9.
On représente un corpuscule non localisé non pas par sa position, car il n'en a pas qu'une seule, mais par ses positions. Comme toutes ses positions ne sont pas équivalentes, cependant, on représente la corpuscule non localisé par un nuage de points plus ou moins dense selon les positions.
Dans l'analogie utilisée précédemment de la petite bille se trouvant "surtout sur votre bureau mais aussi un peu par terre", le nuage de points serait plus dense sur le bureau et moins dense à terre.

Exemple : nuage de points représentant l'électron de l'atome d'hydrogène lorsque ce dernier est dans son "état fondamental" (c'est l'état usuel de l'atome d'hydrogène). les points sont plus denses près du noyau et moins denses loin de ce-dernier. Au-delà d'une certaine distance au noyau, la densité de points est négligeable.
Figure 10.
Cet exemple montre que l'électron n'est pas localisé en un seul point, comme un corpuscule physique classique.
Le caractère non localisé d'une onde classique est un des éléments permettant l'existence d'interférences, qui sont des interactions d'une onde avec elle-même. De façon analogue, le caractère non-localisé de l'électron est à l'origine des phénomènes d'interférences que l'on a décrits au 1.3.1. : l'électron interagit avec lui-même.
L'image de la "bille non localisée" est simplificatrice, et pourrait amener le lecteur à croire l'électron porteur d'aussi peu d'informations qu'une bille lisse. Il n'en est rien, comme on va le voir au paragraphe suivant.
Etat des particules en physique quantique
Ce que nous venons de dire au 1.3.2. peut se généraliser de deux façons :
- De la même façon que l'électron n'a pas généralement une seule position bien déterminée, mais un état qui inclut plusieurs positions -"certaines plus que d'autres"- (comme dans l'analogie macroscopique de la petite bille qui serait "surtout sur le bureau mais aussi à terre"), ses autres caractéristiques (quantité de mouvement p = m v proportionnelle à la vitesse, mais aussi spin, etc...) ne sont généralement pas bien déterminées. L'électron est généralement dans un état qui inclut plusieurs quantités de mouvement. Dans l'analogie de la petite bille fictive précédente, la bille serait par exemple dans un état qui inclut toutes les vitesses entre 2 cm/s et 7 cm/s... Notre bille fictive pourrait même être dans un état de couleur indéterminé incluant les couleurs jaune, orange et rouge!
- Cette caractéristique majeure de la physique quantique : des états qui sont un mélange de plusieurs états "classiques" (par exemple un mélange de plusieurs positions) s'applique, non seulement aux électrons, mais aussi à toutes les particules à petite échelle : plus précisément, les effets quantiques sont généralement perceptibles pour des objets de la taille d'un électron, d'un proton, d'un neutron, d'un quark, d'un photon...
Les informations dont sont porteuses les particules incluent non seulement l'état de position et d'impulsion, mais aussi l'état de spin, l'état de "couleur" (cette grandeur étant très différente de ce que nous appelons généralement "couleur") pour les quarks, etc.
Observation et localisation ou état de l'électron
Une objection peut être faite à ce que l'on vient de dire. Si l'électron n'est pas localisé, comment se fait-il que, lorsqu'on envoie un électron isolé sur un détecteur, on obtienne un "bip" parfaitement localisé?
La réponse fait appel à une autre des "étrangetés" de la physique quantique. Outre le caractère non localisé des électrons et autres particules quantiques, la physique quantique met en évidence un autre phénomène, assez déroutant, qui est l'influence de l'observateur sur l'objet observé.
Certes, en physique classique, on sait que mesurer quelque chose (la position d'un objet, sa vitesse, etc.) perturbe automatiquement, quoique la plupart du temps très peu, l'objet observé : même si l'on ne fait qu'envoyer un rayon lumineux sur l'objet pour que celui-ci nous le renvoie et ainsi pouvoir l'oberver, on l'a "perturbé" car les photons, lorsqu'ils sont arrivés sur l'objet, lui ont communiqué une quantité de mouvement infinitésimale, certes, mais non rigoureusement nulle.
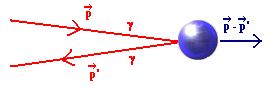
Mesure en mécanique classique de la position d'un objet grâce à la réflexion d'un rayon laser : cette mesure perturbe un peu l'objet, puisqu'elle lui fournit une impulsion égale à p-p', différence d'impulsion des photons incidents et réfléchis. Cette perturbation reste cependant généralement négligeable
Figure 11.
Cependant, en principe, rien n'empêche, en physique classique, de rendre l'influence de la mesure sur l'objet si faible qu'elle soit largement négligeable. Voilà pourquoi, en règle générale, en physique classique, on mentionne rarement l'influence de l'observateur sur l'objet observé.
En physique quantique, par contre, la mesure d'une grandeur (par exemple la position d'un électron) a un effet radical : l'objet observé est généralement fortement perturbé.
Localisation de l'électron après observation de sa position
Considérons un électron, par exemple l'électron d'un atome d'hydrogène qui, avant mesure, est délocalisé comme nous l'avons expliqué précédemment. Après mesure de sa position, l'électron est parfaitement localisé. Cette localisation est une des positions de l'électron délocalisé. Dans l'analogie de la bille qui serait "surtout sur le bureau mais aussi par terre", si on mesure la position de cette bille, après mesure la bille va être localisée, soit sur le bureau, soit par terre.

Lorsqu'on n'observe pas l'électron (ici l'électron d'un atome d'hydrogène), il est délocalisé
Figure 12.
Dès que l'on observe l'électron il a une position bien déterminée
Figure 13.
Peut-on prédire le résultat de la mesure de la position de l'électron quantique ?
Alors qu'on peut déterminer avec une parfaite précision mathématique l'état délocalisé de l'électron avant mesure pour peu que l'on connaisse les conditions initiales, le résultat de la mesure ne peut être prédit qu'en terme probabiliste.
Dans l'analogie de la bille qui serait "surtout sur le bureau mais aussi par terre", si on mesure la position de cette bille, la bille va être localisée après la mesure, soit sur le bureau, soit par terre, on ne peut pas prédire où on la trouvera... On peut juste donner les probabilités de la trouver à chaque endroit. On aura, dans l'exemple en question, plus de chance de trouver la bille sur le bureau que par terre car la bille était "surtout sur le bureau, mais aussi un peu par terre".
De même, le nuage de points représentant la position de l'électron d'un atome d'hydrogène était plus dense près du noyau, donc c'est là que l'on a le plus de probabilité de trouver l'électron.

Figure 14.
Comme, dès qu'on observe sa position, l'électron devient localisé, on ne l'observe jamais dans son état délocalisé, on peut seulement inférer son état des nombreuses observations physiques qui ont été faites et qui, à ce jour, n'ont fait que confirmer la physique quantique.
Une physique aussi étrange peut-elle être vraie ?
En fait, ironiquement, en dépit de cette impossibilité d'observer un électron délocalisé, comme la physique quantique est une des théories que les physiciens ont eu le plus de mal à accepter, c'est aussi l'une de celles qui a subi le plus de tests... et, par suite, l'une des théories physiques les mieux confirmées au monde !
Mesure de la vitesse de l'électron
La situation est similaire lorsqu'on cherche à mesurer la vitesse de l'électron : si celle-ci peut être indéterminée avant mesure, après mesure, elle est parfaitement déterminée. On ne peut prédire avec certitude le résultat de cette mesure, mais seulement donner une probabilité. Dans le cas de l'exemple de la bille qui avait une vitesse non déterminée, et dont l'état incluait toutes les vitesses entre 2 cm/s et 7 cm/s, on ne sait pas après mesure si la bille ira à 3 cm/s ou 6,5 cm/s, par contre, on peut dire avec certitude qu'elle n'ira pas à 8 cm/s ou 1 cm/s.
Ainsi, en physique quantique, chaque fois que l'on mesure une grandeur (position, vitesse, etc...), on ne peut prédire le résultat de la mesure qu'en terme probabiliste. Cette mesure modifie l'état de l'objet observé : après mesure, la grandeur correspondante (position, vitesse, etc.) est parfaitement déterminée.
Représentation mathématique de l'état de l'électron
Les propriétés de l'électron en physique quantique sont décrites convenablement en utilisant des outils mathématiques adéquats.
Notre but n'est pas de faire un cours complet de physique quantique. Nous nous abstiendrons donc de rentrer dans les détails, et nous nous limiterons à donner l'expression mathématique de l'état d'une particule quantique comme, par exemple, un électron *.
|ψ> = ∫ ψ(r) |r> dr |
Ce-dernier est décrit par ce que l'on appelle une "fonction d'onde", que l'on note souvent |ψ>, et qui peut s'écrire comme une somme pondérée de toutes les positions possibles de l'électron.
où ψ(r) est une fonction numérique ordinaire* et |r> l'état "l'électron est localisé au point de coordonnées r".
- On a omis l'état de spin de l'électron
- On norme |ψ> en imposant ∫ |ψ(r)|2 dr = 1
Si ψ(r) = 0 pour tout r sauf en une seule position r = r0, cela signifie que l'électron est localisé en r0.
Dans le cas contraire, l'électron n'est pas localisé, puisque sa fonction d'onde |ψ> inclut plusieurs valeurs de r, donc plusieurs positions différentes.
Le nuage de points représentant la position de l'électron est d'autant plus dense que la norme de ψ(r) est importante. En fait, si on veut être plus précis, la densité du nuage est proportionnelle à |ψ(r)|2.

Figure 15.
Mesures :
Supposons que l'on connaisse parfaitement la fonction d'onde |ψ> de l'électron. Cette fonction d'onde décrit parfaitement l'électron à l'instant considéré, mais ne permet pas de prédire le résultat d'une mesure de la position de l'électron : le résultat de cette mesure, en physique quantique, ne peut être décrite qu'en termes probabilistes. Ainsi, la probabilité que le résultat de la mesure soit la position |r0> est |ψ(r0)|2, proprotionnelle à la densité du nuage de points représentant l'électron délocalisé. Après la mesure, la fonction d'onde de l'électron est modifiée (sauf dans le cas d'un électron localisé) : elle est maintenant |ψ>après mesure = |r0>
Les relations d'incertitude
Si on mesure une grandeur (par exemple la position de l'électron), on ne peut généralement pas, en physique quantique, être sûr du résultat : le résultat de la mesure s'exprime en effet, comme nous l'avons vu plus haut, en terme probabiliste.
Si on s'interroge sur la position de l'objet à un instant donné, |ψ(r)|2 représente la probabilité de présence en r, c'est-à-dire la probabilité de trouver l'objet observé au point r, proportionnelle à la densité du nuage de points représentant la localisation de l'objet. En termes statistiques, ce nuage de points peut être décrit par des grandeurs telles que la valeur la plus probable de r (en laquelle la densité du nuage de points est la plus grande), l'incertitude, etc.
Notons Δ r l'incertitude sur r. Cette incertitude traduit grosso modo la taille caractéristique du nuage de points. Δ r est variable selon les situations. Si on mesure la position d'un électron, aussitôt après la mesure l'électron est localisé. Si on refait une seconde mesure, on a donc, à ce moment-là, Δ r = 0. Inversement, dans certaines situations physiques (métal conducteur par exemple), on peut avoir un électron tellement délocalisé que Δ r est infini ou quasi-infini.
Ce que l'on vient de dire s'applique aussi à l'incertitude sur l'impulsion (p = m v proportionnelle à la vitesse v de l'objet et à sa masse m) Δ p...
En physique classique aussi, on a des incertitudes, même si la situation physique est plus facile à appréhender. Ces incertitudes viennent de la précision de la technique utilisée pour mesurer la position de l'objet, ou son impulsion, ou toute autre grandeur qui nous intéresse.
Les relations d'incertitude d'Heisenberg mettent en évidence une différence supplémentaire entre l'incertitude en physique classique et l'incertitude en physique quantique. En physique classique, il est toujours possible de se donner une limite supérieure sur l'incertitude que l'on veut obtenir sur la position et sur l'impulsion d'un objet, et de faire une mesure avec une incertitude inférieure à cette limite. Autrement dit, le produit Δ r Δ p peut être aussi petit que l'on souhaite. En physique quantique, on montre que, quelle que soit la situation physique considérée, Δ r Δ p sera toujours supérieure à une certaine valeur, notée h, et appelée "constante de Planck". Autrement dit, il existe des situations physiques dans lesquelles un électron est parfaitement localisé (Δ r = 0) et il existe des situations physique dans lesquelles un électron a une impulsion parfaitement définie (Δ p = 0), cependant, on ne peut pas avoir les deux à la fois. Plus l'électron est localisé, moins son impulsion est définie, et inversement.
Relation d'incertitude d'Heisenberg
Cette relation entre l'incertitude sur la position et sur l'impulsion : Δ r Δ p > h avec h ≃ 6,63 × 10-34 J.s fait partie des relations que l'on appelle "relations d'incertitude d'Heisenberg".

Figure 16.
Indiscernabilité
Soient deux boules de pétanque absolument identiques : Arrivez-vous à les distinguer l'une de l'autre ?

Figure 17.
Probablement pas, mais même si vous n'arrivez pas à faire la différence entre les deux en cet instant, vous pouvez toujours, au moins en théorie, prendre une des boules de pétanque, et peindre un "1" dessus, puis prendre l'autre et peindre "2" dessus :

Figure 18.
Désormais, vous pouvez distinguer les deux boules de pétanque.
Ainsi, dans la vie courante, si l'on n'arrive pas toujours à faire la différence entre deux objets, il est toujours, du moins en théorie, possible d'imaginer un moyen de les distinguer.
Faisons de même avec les électrons... Voici deux électrons :

Première hypothèse
Figure 19.
Oh, non !!! En fait, les électrons en physique quantique ne sont pas vraiment localisés... Qu'à cela ne tienne, on peut faire un dessin similaire :
Deuxième hypothèse
Figure 20.
Bon il est exact que des électrons sont encore plus difficiles à distinguer que des boules de pétanque... Surtout des électrons délocalisés quantiques, mais n'est-ce pas, tout au moins "en théorie", la même chose ? Ces électrons que, dans la pratique, on ne peut pas discerner, sont probablement théoriquement discernables ?
En fait, ce n'est pas le cas !!
Les résultats des expériences montrent que, même par la pensée, vous ne pouvez pas prendre un électron et "peindre" un "1" dessus puis prendre l'autre et "peindre" un "2" dessus. En fait, vous ne pouvez pas, même par la pensée, choisir un des électrons plutôt que l'autre. Vous savez qu'il y a deux électrons, mais il n'est pas possible d'en choisir un. Non seulement vous n'arrivez pas à les discerner dans la pratique (ce qui est une situation que l'on peut rencontrer en physique classique), mais c'est aussi théoriquement impossible.
On dit que les électrons sont indiscernables...
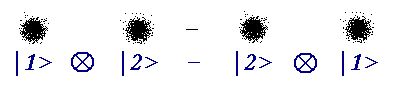
État quantique de deux électrons indiscernables
Figure 21.
L'état de cet ensemble de deux électrons est un mélange de "l'électron 1 est à gauche et l'électron 2 est à droite" et de "l'électron 2 est à gauche et l'électron 1 est à droite"*
Le signe -, qui peut sembler étrange, est une particularité des particules appelées "fermions", comme les électrons, alors que les autres particules quantiques, appelées "bosons", sont caractérisées par un signe plus...
Paradoxe ? Le chat de Schrödinger
La physique quantique, plus encore peut-être que la relativité dont le célèbre "paradoxe" des jumeaux a été fort popularisé (lire à ce sujet l'article « Relativité et vitesse de la lumière »), peut donner lieu à un certain nombre de situations qui semblent paradoxales.
Si l'on a pris l'exemple d'une petite bille fictive, c'était pour aider à comprendre le comportement des électrons, mais aucune bille macroscopique ne se comporte de façon "quantique" comme le fait un électron. En général, donc, la physique quantique, quoique intriguante, parfois perturbante, se cantonne à une partie du monde qui ne fait pas partie de notre quotidien : des électrons invisibles à l'oeil nu, et d'autres particules tout aussi petites...
Cependant, le célèbre "paradoxe de Schrödinger" montre comment on pourrait traduire (au moins dans "une expérience de l'esprit", théoriquement faisable, si ce n'est pratiquement réaliste) les paradoxes microscopiques de la physique quantique, en paradoxes sur des "objets" à notre échelle...
Supposons que l'on mette un chat dans une boite, dans laquelle se trouve une capsule contenant du poison, et dont l'ouverture est commandée par l'état de spin d'un électron. Un électron peut avoir seulement deux états de spin, "up" ou "down", et son état est généralement un mélange de ces deux états. Tant que l'on n'ouvre pas la boite pour observer ce qui se passe, l'électron a à la fois un spin "up" et un spin "down", donc la capsule de poison est à la fois ouverte et fermée, donc le chat est à la fois mort et vivant...
Les dessins ci-dessous illustrent le paradoxe de Schrödinger sous une forme légèrement modifiée, avec des capsules de peintures bleue et rouge plutôt que du poison, commandées par l'état de spin de l'électron (le spin "up" correspondant à l'ouverture de la capsule bleue, le spin "down" à l'ouverture de la capsule rouge) *.
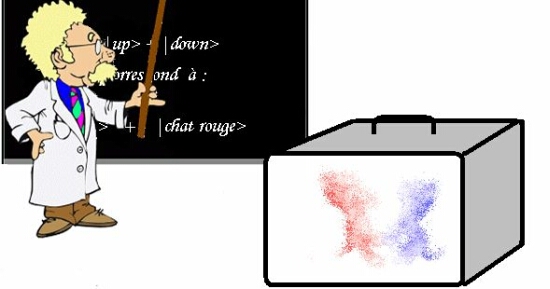
Chat de Schrödinger avant observation : il est à la fois dans l'état "chat bleu" et dans l'état "chat rouge"
Figure 22.

Chat de Schrödinger après observation : sa couleur est bien déterminée... ici, le chat est bleu
Figure 23.
L'auteur de ce texte aime trop les chats pour dessiner l'expérience originale du "chat de Schrödinger" ;)
Les intégrales de Feynman
Présentation
La physique quantique est née du constat de l'existence d'un certain nombre de phénomènes qui ne pouvaient pas être expliqués par la théorie classique qui existait alors. On a montré que la réalité physique contredit la théorie classique, et que la théorie quantique que nous venons d'entrevoir, au contraire, permet d'expliquer et de prédire ces mêmes phénomènes physiques. Cependant, cela ne signifie pas nécessairement que la théorie quantique telle que nous l'avons présentée soit la seule façon de décrire le monde qui nous entoure. En fait, il existe une deuxième présentation de la physique quantique, équivalente à la première : il s'agit des intégrales de chemin de Feynman.
Les intégrales de chemin de Feynman
Dans cette présentation, la probabilité p pour une particule d'aller de la position x1, à l'instant t1, à la position x2, à l'instant t2, peut s'exprimer comme le carré d'une intégrale sur tous les trajets possibles permettant d'aller de (x1, t1) à (x2, t2)
p = |φ2| où φ est appelée "amplitude de probabilité" et φ = ∫trajets e2 π i S(trajet)/h |
où h ≃ 6,63 × 10-34 J.s est la constante de Planck dont on a déjà parlé précédemment, et S est appelée "l'action" et est une fonction du trajet*.
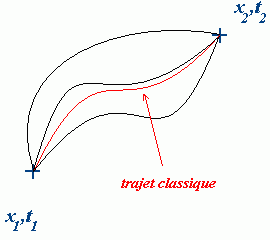
On effectue l'intégrale sur tous les trajets allant de (x1, t1) à (x2, t2), le trajet classique comme les autres trajets classiquement impossibles étant pris en compte.
Figure 24.
L'action est l'intégrale sur tout le trajet du Lagrangien. On a omis, en écrivant l'intégrale sur tous les trajets possibles, de préciser la mesure afin de ne pas alourdir l'écriture mathématique de l'intégrale...
On constate que, puisque h est très petit (de l'ordre de 10-34 J.s!), une variation de S très petite, mais grande devant h, entraîne une très grande variation de la phase dans l'intégrale donnant l'amplitude de probabilité φ. Ces amplitudes ayant des phases très différentes les unes des autres s'annulent mutuellement. Par suite, les seuls trajets qui contribuent significativement à l'intégrale sont les trajets pour lesquels une petite variation de trajet entraîne une variation de l'action petite devant h.
Quel est l'ordre de grandeur de S ?
Dans le cas d'une particule libre (qui n'est soumise à aucune force), on a
S = ∫ m/2 v2 dt |
En ordre de grandeur, l'action est donc de l'ordre de m v2 T où T est le temps mis par la particule pour accomplir le trajet, soit encore S de l'ordre de m v D, où D est la distance parcourue sur le trajet.
Considérons un objet macroscopique de masse m = 1 g, de vitesse v = 1 cm/s, parcourant une distance D = 1 cm, S est alors de l'ordre de 10-7 J.s, très grand devant h. Dans ce cas là, le seul trajet qui contribue un tant soit peu à l'intégrale est celui sur lequel l'action S est extrémale. En effet, c'est le seul trajet pour lequel une petite modification du trajet n'entraine, au premier ordre, pas de modification de l'action. Ce trajet est en fait le trajet classique, et, de fait, conformément aux affirmations de la physique classique, c'est le seul à avoir une probabilité non négligeable.
Si par contre on s'intéresse aux particules subatomiques, comme l'électron, alors les effets quantiques sont beaucoup plus perceptibles. Si on reprend l'ordre de grandeur précédent (S de l'ordre de m v D), mais pour un électron dont la masse est de l'ordre de 10-30 kg, alors, pour v = 1 cm/s et D = 1 cm, on obtient S de l'ordre de 10-34 J.s. Le trajet dont la probabilité est maximale reste bien le trajet classique, correspondant à un extrémum de l'action, mais les trajets suffisamment proches de ce trajet ont à présent une contribution non négligeable.
On voit donc apparaître l'effet quantique que nous avons déjà étudié dans les paragraphes précédents : plusieurs trajectoires différentes sont à prendre en compte, et, par suite, l'électron n'est pas parfaitement localisé.
Conclusion
La méthode des intégrales de chemin de Feynman offre un point de vue alternatif sur la physique quantique : mathématiquement équivalent aux autres points de vues, il permet, dans certains cas, d'obtenir des intuitions ou des résultats plus rapidement sur une situation physique donnée. Ce point de vue met bien en évidence le fait que passer de la physique quantique à la physique classique est équivalent à effectuer l'approximation h → 0.
Conclusion
La physique quantique est l'une des deux révolutions scientifiques majeures du vingtième siècle, avec la théorie de la relativité. Difficile à accepter de par son étrangeté, elle est aujourd'hui une des théories les mieux vérifiées...
Les théories quantiques possèdent cependant des limites sur lesquelles la science travaille encore. Le principal domaine d'activité est l'unification de la relativité générale et de la physique quantique.
Même si la physique quantique a résolu avec éclat les problèmes majeurs du début du vingtième siècle, la construction du savoir des physiciens n'est jamais achevée.
Testez-vous !
Vous pouvez aussi tester vos connaissances grâce à un QCM sur ce que vous venez de lire en allant ici.
Pour citer cet article :
Fenêtre ouverte sur la mécanique quantique, Gabrielle Bonnet, octobre 2004. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Quantique.xml




