L'interaction lumière / particule en 3 questions à Loïc Méès.

Quand un objet est éclairé, il réfléchit ou réémet de la lumière. On parle généralement de diffusion de la lumière. Quand il est transparent, la lumière se propage également à l’intérieur de l’objet, on ne peut plus parler alors uniquement de diffusion, c’est pourquoi le terme d’interaction est plus approprié. De plus, les propriétés physiques de l’objet sont dans certains cas modifiées par la lumière (élévation de température, modification de l’indice de réfraction, destruction, …) et il faut bien alors parler d’interaction. Par particules, on entend des objets de petites tailles. Il ne s’agit pas de particules au sens de la physique atomique mais d’objets dont les dimensions ne sont ni négligeables ni grandes devant la longueur d’onde, disons entre quelques dizaines de nanomètres et quelques centaines de microns. Il existe bien des manières d’étudier ces interactions, expérimentales ou théoriques, mais je vais surtout vous parler des outils, des modèles mathématiques, qui permettent de décrire ces interactions de manière plus ou moins rigoureuses.

Les modèles d’interaction lumière / particule reposent sur l’utilisation de modèles optiques plus généraux. La nature de la lumière et son interaction avec les objets qui nous entourent ont occupé les tout premiers scientifiques. Des modèles d’interaction entre la lumière et la matière basés sur la notion de rayon lumineux existent depuis l’antiquité. Ces modèles qui constituent ce qu’on appelle aujourd’hui l’optique géométrique se sont perfectionnés au cours de l’histoire. Euclide étudie la réflexion, les miroirs et les ombres au III^ème siècle avant notre ère. Il considère des rayons lumineux provenant du « feu intérieur » de chaque être vivant, émis par l’œil en direction des objets observés. Au II^ème siècle de notre ère, Ptolémée étudie la réflexion, la réfraction et les couleurs. Au moyen-âge, c’est dans le monde arabe que nos connaissances en optique progressent. C’est vers l’an 1000 que l’on trouve la première mention d’une loi pour la réfraction (dans un ouvrage d’Ibn Sahl, mathématicien de Bagdad), qui sera redécouverte plus tard en occident. C’est à cette époque également que l’œil est définitivement considéré comme un récepteur et non comme un émetteur de flux lumineux et que les bases de l’optique géométrique telle que nous la connaissons aujourd’hui sont jetées, avec Alhazen, notamment. Au XVII^ème siècle, en Europe, les lois de la réflexion et de la réfraction sont établies par Snell, puis Descartes. C’est aussi à partir de cette époque qu’on attribue une nature ondulatoire à la lumière (avec Huygens et ces ondes lumineuses se propageant dans l’éther) et que cette nature est mise en évidence (avec les anneaux de Newton). C’est au XIX^ème que Maxwell comprend que la lumière est une onde électromagnétique et qu’il décrit son comportement à l’aide d’un ensemble d’équations qui portent son nom. Les équations de Maxwell constituent aujourd’hui le cadre théorique le plus complet et le plus exact pour décrire la propagation des ondes électromagnétiques, des ondes radio aux rayons X, en passant par les ondes visibles de ce large spectre que l’on appelle lumière.

Dans le cadre de mes recherches, l’interaction entre lumière et particule, représente le problème direct. Pour faire de l’optique un instrument de mesure, il faut d’abord comprendre comment la lumière interagit avec un objet, pour ensuite éclairer cet objet, observer la lumière qu’il nous renvoie et en déduire ces propriétés, c’est-à-dire résoudre le problème inverse (voir figure 1).

Source - © 2012 L. Méès

Chaque goutte apparait sous forme d'un disque lumineux. Le nombre de franges contenues dans le disque est une mesure directe du diamètre de la goutte. - @ L. Méès

Figure 1. Image de gouttes d'eau par imagerie interférométrique en défaut de mise au point

Différents modèles permettent de décrire l’interaction lumière / matière. Le plus ancien, l’optique géométrique peut tout à fait être utilisé pour décrire l’interaction de la lumière avec des objets de grande taille (devant la longueur d’onde), sous une forme plus ou moins élaborée selon les objectifs. La diffusion par les très petites particules, atomes ou molécules peut-être calculée à l’aide du modèle de Rayleigh qui décrit la réponse d’un dipôle unique à une onde électromagnétique. Pour des objets de taille intermédiaire, dont les dimensions sont typiquement comprises entre quelques nanomètres et quelques centaines de microns, il est nécessaire de travailler dans un cadre électromagnétique avec des modèles plus complexes ou une modélisation purement numérique (basée sur une discrétisation du temps et de l’espace).

Le dipôle électrostatique est une entité constituée de deux charges. Il peut être induit par un champ électromagnétique, par déformation du nuage électronique d’un atome ou d’une molécule par exemple. On parle alors de polarisation.

Je pourrais faire une réponse très générale : tout dépend de ce que l’on veut en faire. Selon la taille de l’objet, sa forme ou les propriétés de diffusion auxquelles on s’intéresse, on ne choisira pas le même modèle. L’optique géométrique fonctionne bien pour les objets assez gros. Les particules dont je parle ici ont des dimensions qui s’approchent en ordre de grandeur des longueurs d’onde du visible. Ce sont par exemple : des poussières, des cristaux de glace, des gouttes d’eau, des bulles, des fibres de verre, … Ces objets sont généralement trop petits pour que l’on puisse décrire correctement leur interaction avec la lumière par l’optique géométrique et ils sont trop gros pour être considérés comme un dipôle unique.

En plus des limitations sur la taille de la particule, l’optique géométrique présente l’inconvénient de ne pas tenir compte de certains phénomènes, comme la diffraction, ou les phénomènes d’arc-en-ciel. L’idéal, c’est de traiter le problème de l’interaction lumière / particule dans le cadre théorique le plus rigoureux (l’électromagnétisme), mais c’est une chose de connaitre les équations qui régissent la propagation des ondes, de poser le problème de leur interaction avec une particule donnée, c’en est une autre de pouvoir résoudre ce problème. Même dans un cadre théorique rigoureux, il est donc nécessaire de faire des hypothèses qui limitent les conditions d’application des modèles.

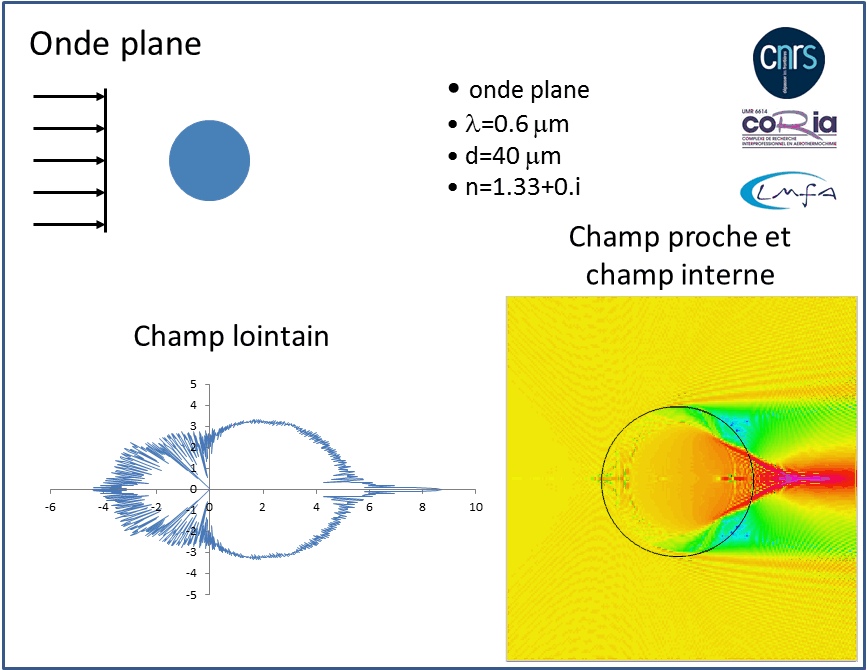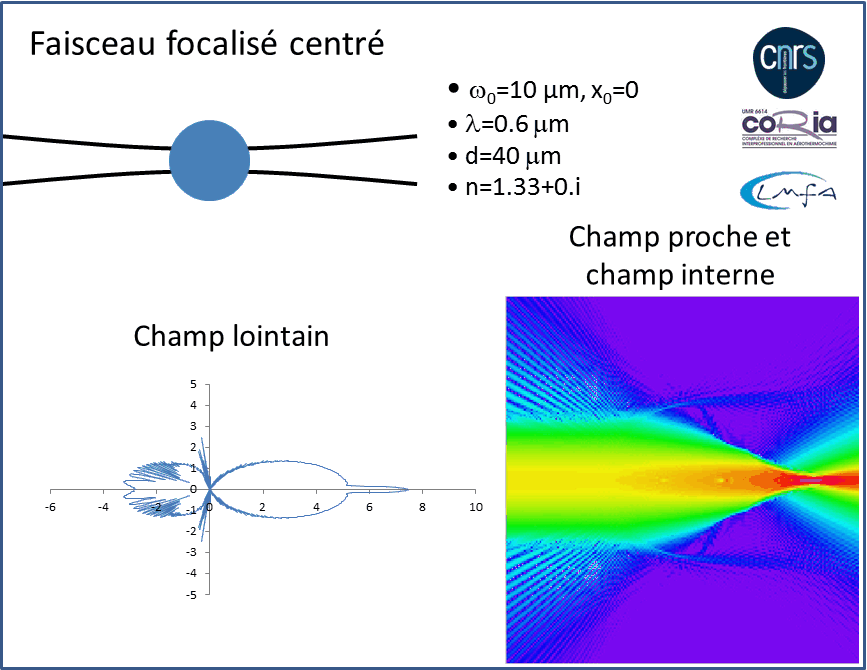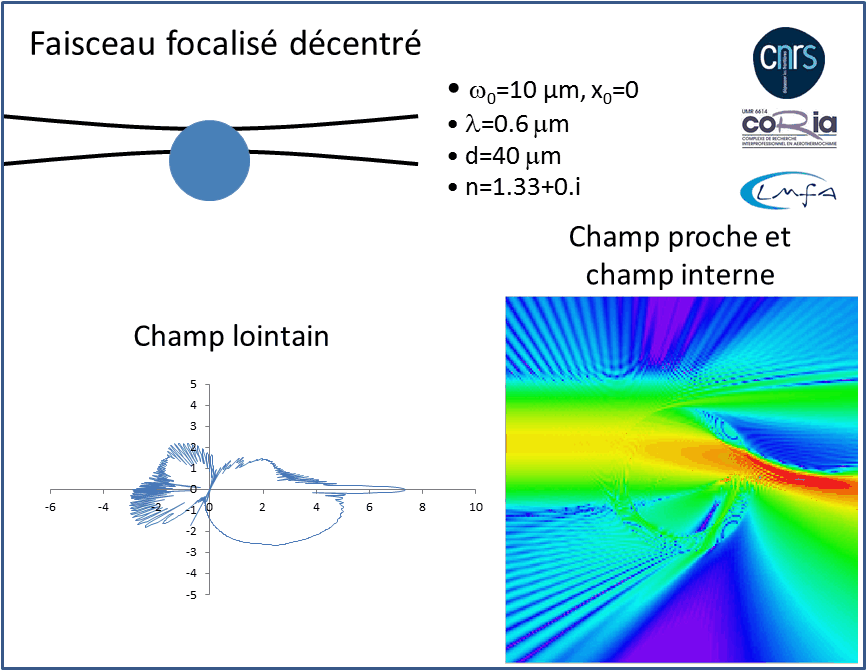
Un modèle avec lequel j’ai beaucoup travaillé est la Théorie de Lorenz-Mie (TLM). La théorie de Lorenz-Mie a la particularité d’avoir été développée en parallèle par Lorenz à la fin du XIXème siècle et par Mie au début du XX^ème siècle, de manière complètement indépendante. Lorenz s'est placé dans le cadre de la théorie de l’éther qui est désormais oubliée, et Mie dans le cadre de l’électromagnétisme et des équations de Maxwell. On parle de Théorie de Lorenz-Mie mais il s’agit en fait de la solution mathématique à un problème, celui de l’interaction entre une onde électromagnétique plane (éclairage uniforme) et une particule parfaitement sphérique. Ce modèle a ceci de puissant qu’il est sans limitation de taille ni d’indice de réfraction. C’est un modèle qui permet de considérer les plus petits objets comme les atomes ou les molécules (la solution de Lorenz-mie tend vers celle de Rayleigh quand la taille de la particule devient négligeable devant la longueur d’onde) et les plus gros objets que l’on peut décrire avec l’optique géométrique.

Source - © 2012 L. Méès

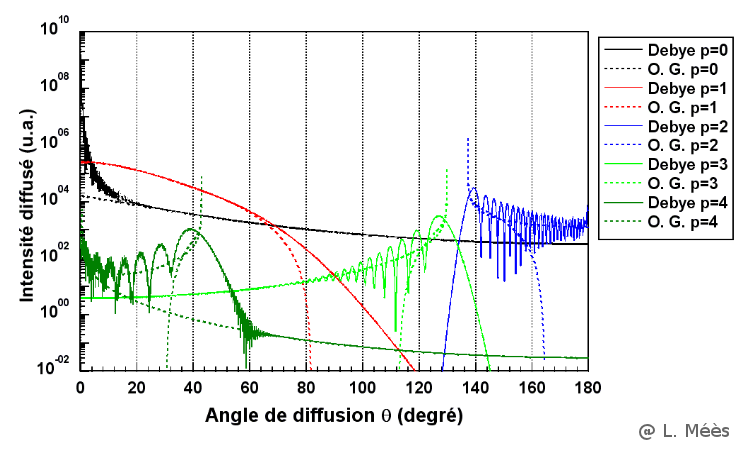
Les calculs issus d'Optique Géométrique (O.G. sans prise en compte des interférences) et de la Théorie de Lorenz-Mie (avec décomposition de Debye) sont comparés pour les premiers ordres de diffusion (p =0 : réflexion/diffraction, p = 1 : réfraction, p > 1 : réfraction après p-1 réflexions internes). - @ L. Méès

Figure 2. Diagramme de diffusion d'une goutte d'eau de 60 μm éclairée par une onde plane (λ= 532 nm)

Cette théorie et les nombreuses approches dérivées permettent de décrire les interactions lumière / particules sans hypothèse, à priori, sur la taille ou l’indice de réfraction de la particule. Par contre, ces modèles se réduisent aux interactions linéaires et élastiques entre la lumière et des particules de forme régulières.

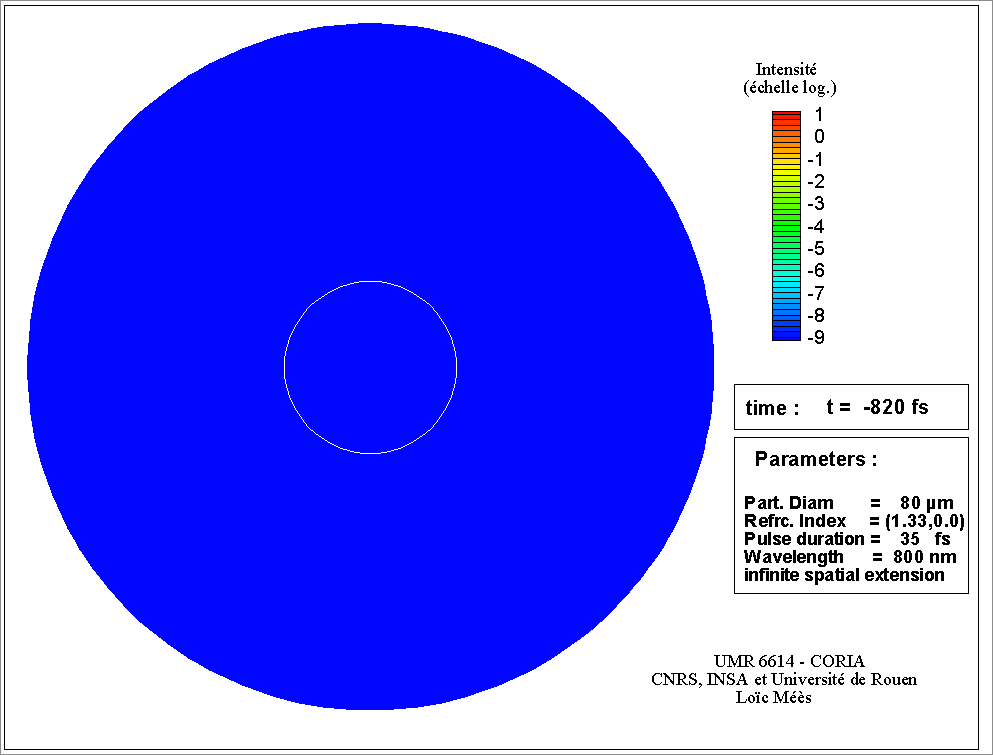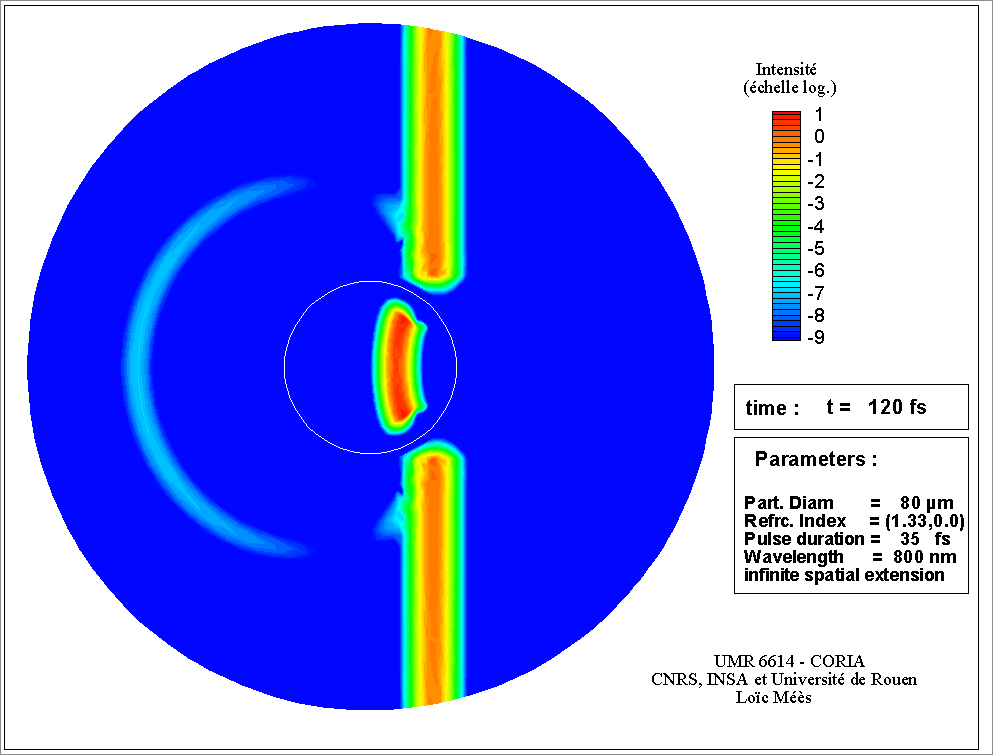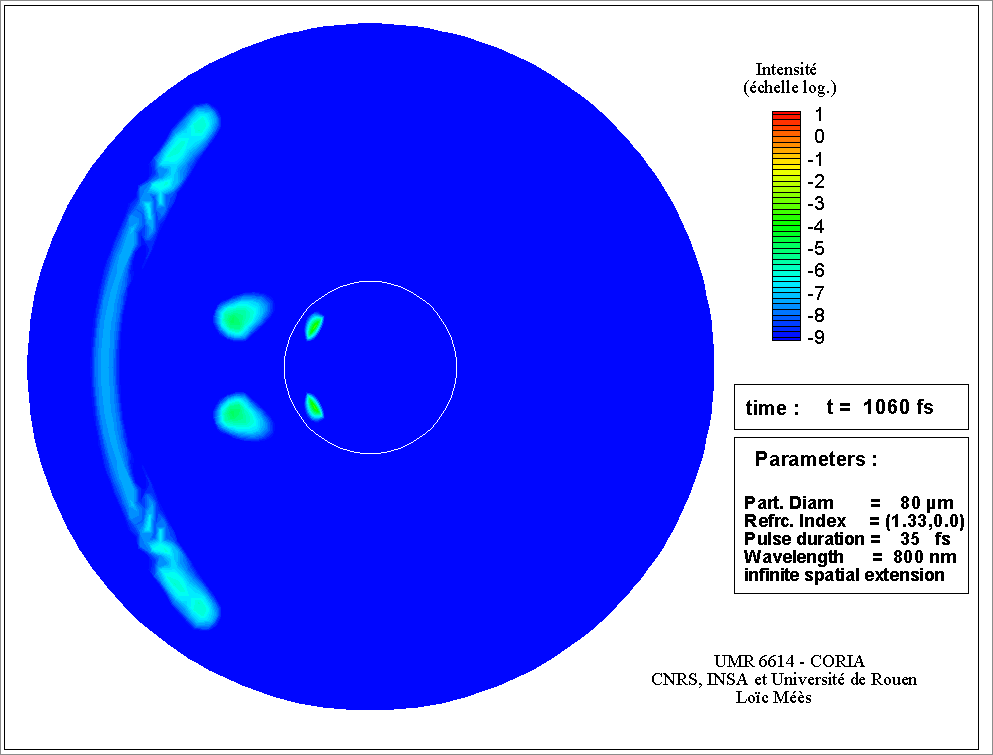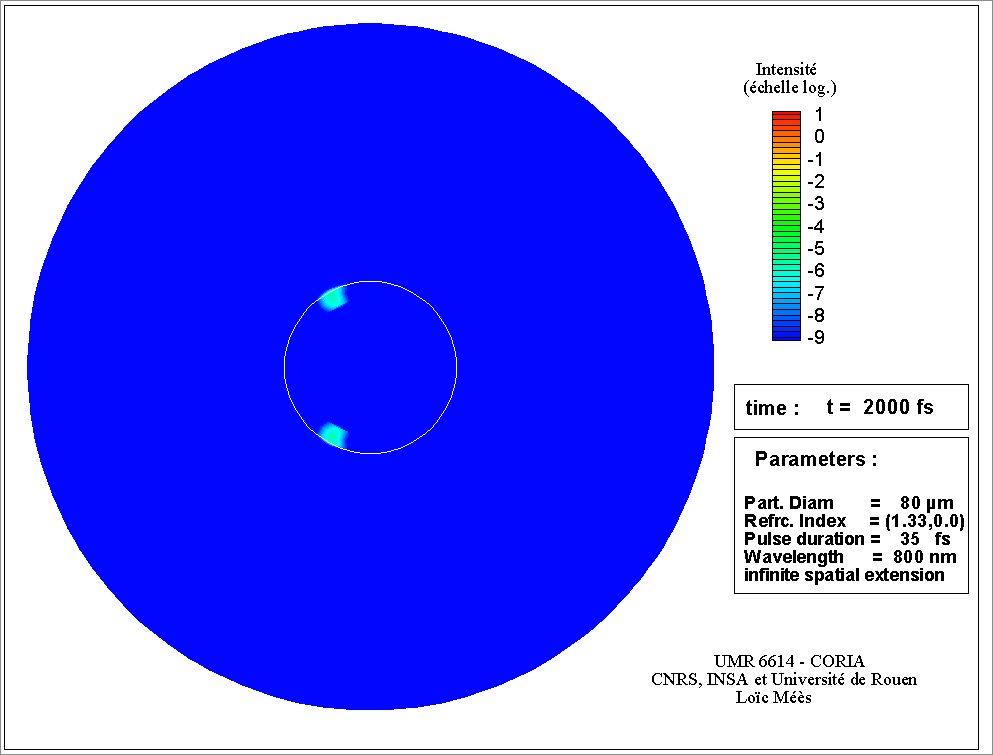
La TLM est la base de nombreux modèles de diffusion. J. R. Wait (1955) à développé l’équivalent de la théorie de Lorenz-Mie pour un objet cylindrique. Des formulations pour des particules de forme sphéroïdale, pour un cylindre de section elliptique (c’était l’objet de ma thèse), pour des particules sphériques à couches, ou avec des gradients d’indice. Avec la place croissante qu’occupent les Lasers dans les sciences modernes, l’hypothèse de l’onde plane (éclairage uniforme) a également due être levée, pour considérer des faisceaux focalisés. On parle alors de Théories de Lorenz-Mie Généralisées (voir animation sur la figure 3). La TLM a également inspirée une autre famille de modèles qui font d’avantage appel au calcul numérique mais qui permettent de prendre en compte des formes plus exotiques (cristaux, ensembles de sphères ...). Ces modèles utilisent la méthode de la matrice T ou méthode des conditions aux limites étendues. Ces méthodes sont limitées à des objets de tailles plus réduites tout comme le sont les méthodes purement numériques, basées sur une discrétisation de l’espace et du temps.

Source - © 2012 L. Méès

Calcul du champ interne et du champ proche dans une section de l’espace par Théorie de Lorenz-Mie généralisée. - @ L. Méès

Figure 3. Interaction entre une goutte d’eau de 40 µm et un faisceau laser focalisé

Le choix du modèle le plus approprié dépend ainsi de la taille et de la forme des particules. La TLM et les modèles équivalents sont les plus rigoureux et ils servent généralement de référence pour valider l’utilisation d’un modèle plus simple dans un contexte donné. Par exemple, pour calculer la fréquence des franges d’interférence crées par une goutte, à 30° de la direction du faisceau incident, un modèle d’optique géométrique qui ne considére que les rayons réfléchis et réfractés par la goutte peut-être suffisant. Pour savoir jusqu’à quels angles et à partir de quelle taille de particule ce modèle simple est applicable on le compare à des calculs de Théorie de Mie. Ce modèle simple peut alors être utilisé en parfaite connaissance de ses limites, pour inverser le résultat d’une mesure et en déduire, toujours dans l’exemple précédent, la taille de la goutte avec une grande précision.

En plus de leur limitation à des formes de particules régulières, les modèles du type TLM ont deux inconvénients. D’abord ils ne sont pas facilement réversibles. A partir d’une mesure de la lumière diffusée dans une direction donnée, il n’est pas possible de faire un calcul inverse de Théorie de Mie pour retrouver les propriétés de la particule (sa taille par exemple). Il est toujours possible de réaliser un grand nonmbre de calculs et d’en tabuler les résultats, mais si un modèle plus simple, réversible est utilisable, on le choisira. Ensuite, la TLM n’est pas très intuitive car elle fournit une réponse globale de la particule à l’onde qui l’éclaire. Avec l’optique géométrique, on est capable suivre l’interaction en terme de trajectoire lumineuse, en suivant les rayons réfléchis et réfractés à chaque interface, réfléchis plusieurs fois à l’intérieur de la particule avant d’en ressortir dans une direction donnée. Il est alors plus simple d’interpréter physiquement l’influence de légères modifications de l’indice de réfraction (de température) de la taille ou de la forme de la particule qu’à l’aide de la TLM ou de son équivalent pour une particule de forme sphéroïdale.

En résumé, si on cherche à comprendre un comportement dans ses grandes lignes, « avec les mains », on utilisera un modèle d’optique géométrique. Et si au contraire on a besoin d’une grande précision dans la description de la lumière diffusée, avec les interférences, et les effets « purement ondulatoires » comme la diffraction ou les ondes de surface, on utilisera une approche de type Théorie de Lorenz-Mie. Pour les particules de forme irrégulière, on utilisera des méthodes numériques. Enfin, pour traiter des effets non linéaires de l’interaction, seules les approches purement numériques semblent pouvoir être utilisées. A ma connaissance cependant, elles ne permettent pas, ou pas encore, de traiter des cas pratiques, utiles à la communauté scientifique. Cette question reste donc ouverte.

Les applications se trouvent principalement dans les domaines de la métrologie et de l’imagerie. Beaucoup sont liées à la mécanique des fluides ou à l’astronomie. En astronomie d’abord, les poussières interstellaires, les poussières de notre atmosphère ou de celles d’une autre planète, les nuages, les gouttes d’eau ou les cristaux de glace sont autant de particules (au sens où nous l’avons défini) qui peuvent modifier les images ou les mesures réalisées par les télescopes. Des modèles de diffusion sont nécessaires pour comprendre et quantifier ces modifications, afin de corriger les images de l’espace prises du sol ou d’analyser la surface ou l’atmosphère d’une planète. Dans l’autre sens, on cherche également à corriger les images du sol qui sont prises depuis l’espace ou les hautes couches de l’atmosphère, pour des applications liées à la localisation, à la météorologie ou aux activités militaires.

Ces modèles d’interaction lumière / particules sont également très utilisés en métrologie (mesure) et dans le domaine de la mécanique des fluides en particulier. L’optique est en effet un moyen de mesure in situ, non intrusif et précis pour analyser des particules solides, les gouttelettes d’un spray ou des bulles, directement dans un écoulement. Le principe de ces mesures est simple : les particules sont éclairées, le plus souvent à l’aide d’un laser, et on mesure la lumière diffusée dans une direction donnée. La lumière diffusée est analysée à l’aide d’un modèle de diffusion et on remonte aux propriétés des particules. De nombreuses techniques de mesure sont basées sur ce principe, comme l’Anémométrie Phase Doppler, la réfractométrie d’arc-en-ciel ou d’autres techniques de type interférométriques qui permettent de mesurer la taille de fibres ou de gouttes en écoulement. Les modèles d’interaction lumière / particules tiennent une place essentielle dans le développement de ces techniques de mesure. On peut même ajouter que le développement de ces modèles a été en grande partie motivé par les applications métrologiques.

Ces théories sont relativement anciennes (Lorenz 1891, Mie 1908, Debye 1917). Pendant très longtemps elles n’ont pas suscité d’engouement particulier et ce pour 2 raisons : La première est l’absence de moyens de calcul. A l’époque les premiers calculs ont été réalisés à la main, ils étaient très laborieux. Des jours, voir des semaines de calculs étaient nécessaires pour des tailles de particules qui dépassaient à peine la longueur d’onde. L’autre raison, c’est l’utilité toute relative que ces travaux présentaient. Les sources de lumière monochromatique étaient très difficiles à mettre en place, peu intenses, à faible longueur de cohérence et n’offraient pas de possibilité d’application de ces modèles.

Ces deux 2 freins ont disparu à peu près en même temps, dans les années 1960, avec l’avènement, d’une part des moyens de calcul modernes et d’autres par de celui des lasers. Les moyens de calcul se sont développés à la vitesse que l’on sait, permettant de considérer des tailles de particules plus importantes et ainsi répondre à un besoin lui aussi en plein développement, grâce aux progrès des sources lasers. Ces lasers produisent une lumière quasiment monochromatique, facile à collimater et puissante. Ils ont ouvert de nouvelles perspectives en matière de métrologie. Les progrès réalisés en termes de puissance et de variétés des longueurs d’onde disponibles, n’ont pas cessés depuis les années 60, ce qui s’est traduit par une multiplication des applications métrologiques et des besoins en matière de modélisation. Aujourd’hui encore, les sources impulsionnelles ultra-brèves, de l’ordre de la femtoseconde (10^-15 s), renouvellent ces besoins. Les aspects temporels des phénomènes d’interaction, jusqu’ici négligés prennent toute leur importance, et encouragent le développement de nouveaux modèles ou leur extension à ces nouvelles réalités (voir animation figure 4). Ces impulsions délivrent également une puissance instantanée colossale qui remet en cause les hypothèses d’une interaction élastique et linéaire et propose aux chercheurs un nouveau défi en matière de modélisation.

Une femtoseceonde est à une seconde ce qu’une seconde est à 31 Millions d’années. La lumière qui se propage a une vitesse prodigieuse, certes finie, mais la plus grande qui soit, ne parcours que 30 microns en 100 fs dans l’air.

Source - © 2012 L. Méès

@ L. Méès

Figure 4. Interaction entre une impulsion de 35 fs et une goutte d’eau de 80 µm de diamètre

On peut également citer une autre application, loin du domaine de la métrologie ou de l’imagerie, ce sont les « pincettes optiques ». La lumière applique une force sur les particules qu’elle éclaire selon un principe d’action/réaction. Si on éclaire un objet de manière suffisamment intense cet objet peut être mis en lévitation. A l’aide de faisceaux très focalisés, il est même possible d’attraper cet objet et de le déplacer ou de le manipuler. Ces pincettes optiques sont utilisées aujourd’hui pour manipuler des cellules vivantes, ou réaliser des essais de traction sur des brins d’ADN. Les modèles d’interaction lumière / particule les plus rigoureux (Théorie de Lorenz-Mie généralisées) sont utilisés pour mettre au point ces techniques, quantifier les forces de pression, de radiation et les couples exercés sur les particules.