Activer le mode zen
Ressource au format PDF
Mots-clés
- niveau d'énergie
- atome polyélectronique
- atome hydrogénoïde
- charge
- rayons X
- loi de Moseley
Classification
Énergie des atomes polyélectroniques et coefficient d'écran
04/03/2005
Résumé
L'énergie des atomes polyélectroniques, du fait des interactions entre électrons, est très difficile à calculer. Une approximation, l'approximation du champ central, qui fait intervenir des coefficients appelés "coefficients d'écran", permet toutefois d'accéder à une approximation de ces niveaux d'énergie. Cette théorie est aussi utile pour comprendre le spectre d'émission des rayons X, et en particulier la loi de Moseley.
Table des matières
Le coefficient d'écran apparaît à la fois en physique atomique, lors du calcul du rayon d'un atome ou d'un ion, et en spectroscopie à rayons X. Mais de quoi s'agit-il ? Qu'est-ce qu'il signifie ?
Atome d'hydrogène et ion hydrogénoïde : rappels
Un des premiers calculs que l'on effectue en physique atomique est le calcul des niveaux d'énergie de l'atome d'hydrogène, car le système est simple : un noyau et un électron seulement en interaction. Si l'on calcule l'énergie de ce système, on trouve que les niveaux d'énergie possibles de l'atome d'hydrogène sont caractérisés par En = - R/n2 où n = 1, 2, 3, ... et où R est la constante de Rydberg qui vaut R = 13,6 eV.
Un calcul tout aussi simple donne les niveaux d'énergie des ions hydrogénoïdes, c'est-à-dire des ions constitués d'un noyau de charge Z, et d'un seul électron tournant autour de ce noyau. Les niveaux d'énergie d'un ion hydrogénoïde sont similaires à ceux de l'atome d"hydrogène : on a : En = - R Z2/n2, où Z est le nombre de charges de l'élément considéré, Z-1 étant la charge de l'ion hydrogénoïde correspondant.
Atome ou ion polyélectronique
Comment faire, cependant, lorsqu'un atome ou un ion est entouré par un grand nombre d'électrons ? Ces électrons ne sont pas indépendants, et un calcul exact de l'énergie de l'atome ou de l'ion devrait donc tenir compte de tous ces termes d'interaction électrostatique.
Introduction : le problème :
Considérons l'énergie d'un atome à Z électrons. Si on note me la masse d'un électron, et si on définit, pour simplifier les écritures, e via la relation : e2 = q2 /(4 π ε0), alors on peut écrire l'énergie de l'atome (ou, de façon similaire, son Hamiltonien en terme d'opérateurs) :
E ( ou alternativement, en terme d'opérateurs, H) = ∑i Pi2/(2 me) - ∑i (Z e2)/Ri + ∑i < j e2/|Ri - Rj| |
Pi est la quantité de mouvement de l'électron i, ou l'opérateur quantité de mouvement si on écrit non pas l'énergie classique de l'atome mais son hamiltonien.
Le premier terme de l'expression ci-dessus correspond à la somme des énergies cinétiques des Z électrons de l'atome, le second terme est la somme, sur les Z électrons, du potentiel d'interaction entre le noyau (de charge Z q) et les électrons (chacun de charge - q). Comme q2 /(4 π ε0) = e2, on n'a pas besoin de faire intervenir explicitement dans l'expression du potentiel le coefficient ε0. Enfin, le troisième terme, qui comprend une somme sur toutes les paires {i,j} d'électrons, décrit le potentiel d'interaction entre électrons.
A ce stade, on constate qu'il serait beaucoup plus simple de calculer l'énergie de l'atome si le dernier terme n'existait pas. En effet, si c'était le cas, les électrons seraient totalement indépendants, et on se retrouverait à faire la somme des énergies correspondant à chacun de ces électrons, ces énergies ayant été calculées précédemment (ce sont les mêmes que pour les ions hydrogénoïdes de nombre de charge Z).
Si on compare le troisième terme au deuxième, on se rend compte que le deuxième, en approchant Ri par la distance moyenne d'un électron à l'atome a, donne, après avoir effectué la somme sur tous les électrons de l'atome : Z2e2/a. Si on assimile, pour estimer le troisième terme, |Ri - Rj| à a, et une fois la somme sur les Z(Z-1)/2 paires d'électrons effectuée, on obtient Z(Z-1) e2/(2 a), qui est même ordre de grandeur que le deuxième terme.
Un calcul approché en négligeant les termes d'interaction entre les électrons ne se justifie donc pas, et un calcul en perturbation non plus, puisque la perturbation serait pour la majeure partie des atomes très proche (de l'ordre de 1/4 au mieux, 1/2 au pire) du terme non-perturbatif...
L'approximation du champ central
Imaginons un court instant que l'un des électrons, de la couche la plus externe de l'atome, soit très éloigné à la fois du noyau et des autres électrons. Quel potentiel "verrait-il" à cette distance ?
En fait, à très grande distance, le noyau et les Z-1 autres électrons sembleraient quasiment au même endroit, et la charge "perçue" par l'électron serait "écrantée" par la présence de Z-1 électrons... cette "charge effective" perçue par l'électron serait de Z (charge du noyau) - (Z-1) (charge des autres électrons) = 1. Ou pourrait alors déterminer simplement l'énergie de cet électron, puisque tout se passerait finalement comme si on avait un atome d'hydrogène (une seule charge positive q au centre, et une charge négative, l'électron, en orbite autour de ce noyau).
Cette approximation montre très vite ses limites sous cette forme-ci, puisque l'approximation ne sera plus valable si l'électron est plus proche du noyau et des autres électrons, ou, par suite, pour les électrons des couches internes. Toutefois, c'est une version adaptée de cette aproximation qui est couramment utilisée en physique : l'approximation du champ central.
Charge efficace du noyau et coefficients d'écran : définitions
Dans cette approximation, Les électrons en orbite autour d'un noyau de nombre de charges Z ne "voient" pas cette charge complète, mais une charge plus faible, car les électrons situés sur des orbites plus basses, de charge négative, font "écran" à la charge du noyau.
La charge efficace du noyau, vue par l'électron i, est donc inférieure à Z, elle vaut :
Z*i = Z - ∑j ≠ i εji |
εji est appelé "coefficient d'écran", il dépend des électrons i et j, et décrit l'effet d'"écran" exercé par l'électron j sur l'électron i.
Z*i est la charge nucléaire effective perçue par l'électron i.
L'énergie de l'électron i se déduit de celle d'un atome hydrogénoïde en remplaçant Z par Z*i. L'énergie totale de l'atome, à son tour, est obtenue en faisant la somme des énergies de chaque électron, supposés, dans ce modèle, être indépendants.
Pour pouvoir obtenir le résultat, dans l'approximation du champ central, il suffit donc de connaître le coefficient d'écran correspondant à chacune des paires d'électrons.
Variation du coefficient d'écran avec les positions respectives des électrons i et j
On pourrait supposer, en première approximation, que chaque électron situé sur une orbite plus haute que celle de l'électron i considéré a un coefficient d'écran correspondant égal à 0, et que chaque électron situé sur une orbite plus basse contribuerait pour 1 au coefficient d'écran. Ainsi, la charge efficace serait égale à Z - nombre d'électrons sur des orbites plus basses que l'électron considéré.
Cependant, les électrons j proches de l'électron i, placés sur des orbites plus basses, ont un coefficient d'écran inférieur à 1.
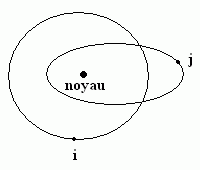
On peut le comprendre en se référant aux orbites classiques (qui ne représentent pas la réalité mais permettent malgré tout de "deviner" le résultat). Un électron sur une orbite elliptique va pouvoir, en certains points de son orbite, entrer à l'intérieur de l'orbite d'un électron d'énergie inférieure. A ce moment, la charge du noyau ne sera donc plus vraiment "écrantée" par l'électron d'énergie plus basse.
En réalité, les électrons sont quantiques et ne suivent pas des orbites classiques, pour autant, ce raisonnement est utile pour comprendre comment la contribution des électrons d'énergie inférieure à celle de l'électron considéré peuvent correspondre à des coefficients d'écran différents de 1...
Valeurs des coefficients d'écran
Le modèle de Slater donne une approximation du coefficient d'écran selon les paires d'électron. Bien que cela ne permette de calculer qu'une approximation de l'énergie réelle des atomes, la rapidité avec laquelle cette méthode permet d'obtenir des résultats est très intéressante.
Dans le modèle de Slater, les électrons sont classés par groupes : 1 s; 2 s et 2 p; 3 s et 3 p; 3 d; 4 s et 4 d; 4 f; 5 s et 5 p...
Pour un couple (i,j), tel que l'électron j soit dans un groupe supérieur à celui de l'électron i, alors εji = 0
Pour un couple (i,j) tel que l'électron j soit dans le même groupe que l'électron i, alors εji = 0,31 si i et j sont dans l'état 1s, εji = 0,35 sinon.
Pour un couple (i,j) tel que l'électron j soit dans le groupe juste en-dessous de celui de l'électron i, alors εji = 0,85
Enfin, pour un couple (i,j) tel que l'électron j soit dans un autre des groupes inférieurs à celui de l'électron i, on a εji = 1
Application : loi de Moseley
Le coefficient d'écran peut servir, bien entendu, à calculer une approximation des énergies des atomes polyélectroniques.
On le retrouve aussi, cependant, lorsqu'on produit des rayons X par bombardement d'un métal avec des électrons. Le spectre électromagnétique obtenu dans ces conditions est la superposition d'un spectre continu (l'énergie cinétique de l'électron est partiellement convertie en énergie électromagnétique) et d'un spectre de raies. C'est le spectre de raies qui nous intéresse ici en relation avec le coefficient d'écran.
Déterminons tout d'abord, dans un premier temps, l'énergie de transition entre deux niveaux dans le cas d'ions hydrogénoïdes. Comme les niveaux électroniques ont une énergie :
En = - R Z2/n2
L'énergie électromagnétique émise lors d'une transition entre deux niveaux est donc proportionnelle à Z2. Cette proportionalité est intéressante dans la mesure où elle permet, en fonction du spectre émis, de déterminer la nature de l'ion considéré.
Dans le cas d'atomes polyélectroniques, nous avons vu que la situation est très proche, à ceci près, qu'en première approximation, Z va être remplacé par Z*, qui correspond à Z diminué d'un coefficient d'écran...
C'est effectivement ce qu'a constaté Moseley en 1913 : l'énergie des photons émis est proportionnelle à (Z - constante)2
Cette constante correspond à l'"écrantage" exercé sur l'électron qui fait la transition (dans la pratique, il s'agit le plus souvent d'une transition entre la couche 1 et la couche 2). On retrouve donc le résultat de la théorie développée dans les paragraphes précédents.
Conclusion
Ainsi, du calcul de l'énergie des atomes polyélectroniques à la loi de Moseley décrivant le spectre d'émission des rayons X, l'approximation du champ central permet de comprendre et d'obtenir des résultats sur un problème pourtant extrêmement complexe, celui d'électrons fortement corrélés entre eux.
Pour en savoir plus sur l'approximation du champ central, voir : "Mécanique Quantique II", Cohen-Tannoudji, Diu, Laloë, Hermann éditeur, p 1404 à 1411.
Pour citer cet article :
Energie des atomes polyélectroniques et coefficient d'écran, Gabrielle Bonnet, Marie-Christine Artru, mars 2005. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Ecran.xml