Activer le mode zen
Ressource au format PDF
Mots-clés
- rayonnement
- diffraction
- loi de Bragg
- condition de Laue
- monocristal
Classification
Diffraction des rayons X
Techniques et études des structures cristallines
28/10/2009
Résumé
Bases théoriques de l'interaction des rayons X avec des structures solides et mises en oeuvre d'exemples d'applications : résolution de structure cristalline sur monocristaux et reconnaissance de phases dans des solides cristalisés.
Table des matières
Introduction
Découverts en 1895 par le physicien allemand Röntgen, les rayons X sont à la base de différentes techniques d'analyse comme la radiographie, la spectroscopie et la diffractométrie. Ces radiations électromagnétiques ont une longueur d'onde de l'ordre de l'Ångström (1 Å = 10-10 m).
Un cristal est un agencement d'atomes, d'ions ou de molécules, avec un motif se répétant périodiquement dans les trois dimensions. Les distances interatomiques sont de l'ordre de l'Ångström, du même ordre de grandeur que les longueurs d'onde des rayons X : un cristal constitue donc un réseau 3D qui peut diffracter les rayons X.
En 1913, William Lawrence Bragg et son père Sir William Henri Bragg utilisèrent ce rayonnement pour déterminer la structure cristalline de NaCl puis celles de nombreux autres sels métalliques. Ils reçurent conjointement le prix Nobel de Physique en 1915 pour leurs contributions à « l'analyse de la structure cristalline au moyen des rayons X ».
Nous présentons la théorie de base de l'interaction des rayons X avec des structures solides ainsi que la mise en oeuvre d'exemples d'applications : la résolution de structure cristalline sur monocristaux et la reconnaissance de phases dans des solides cristalisés.
Interaction des rayons X avec la matière
Production des rayons X pour la diffraction
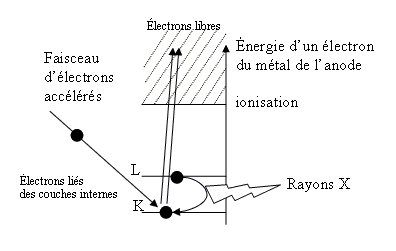
La production des rayons X se fait généralement suivant le même procédé que celui utilisé en imagerie médicale. Des électrons arrachés à un filament de tungstène chauffé électriquement sont accélérés sous l'effet d'un champ électrique intense (tension de 50 kV) pour bombarder une anode (ou anticathode) faite de matériaux différents selon les applications visées. Les rayons X sont émis par l'anode selon deux mécanismes détaillés dans l'article « La radiographie II. Qu'est-ce qu'un rayon X ? Comment en produire ? Quel mécanisme permet d'obtenir une radiographie ? ».
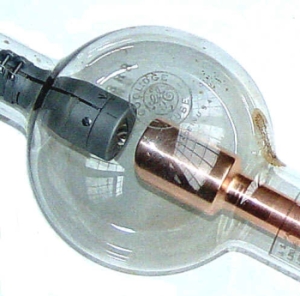
Figure 2. Tube de Coolidge |
Les deux métaux couramment utilisés pour l'anode sont le cuivre, qui produit des rayons X de longueur d'onde λ = 1,54 Å et le molybdène, λ = 0,709 Å. Comment choisir le matériau ? Pour avoir une diffraction optimale, il faut utiliser un rayonnement de longueur d'onde du même ordre de grandeur que la taille du réseau, ici l'espace interatomatique. C'est pourquoi les sources à base de molybdène sont adaptées à la résolution de structure sur monocristal de petites molécules. On utilise le cuivre dans le cas des macromolécules (comme une protéine) et pour les analyses de poudres car il permet une meilleure séparation des taches de diffraction.
Une autre source de rayonnement X est le synchrotron. En effet toute particule chargée en mouvement émet un rayonnement électromagnétique continu (le rayonnement synchrotron) couvrant une large gamme de fréquence de l'ultraviolet lointain au rayon X. L'intensité du rayonnement synchrotron dépasse largement celle des autres sources. L'usage d'un tel instrument est réservé aux cas les plus difficiles, pour mettre en évidence des détails très fins ou pour caractériser des cristaux aux dimensions très faibles (de l'ordre de la dizaine de micromètre).
Diffraction des rayons X
1. La loi de Bragg
Un cristal peut être vu comme la répétition périodique tridimensionnelle
d'éléments (atomes ou molécules), appelés nœuds, repérés par des disques noirs sur
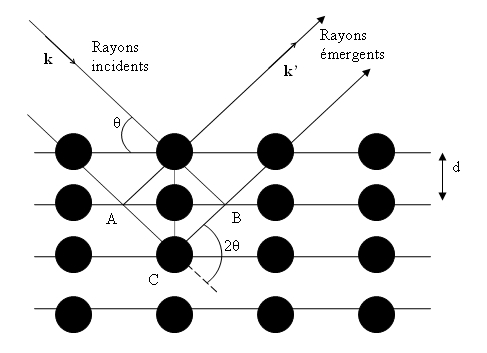
la figure 3. Le schéma représente une coupe de plans
réticulaires passant par les centres de ces éléments, espacés d'une
distance d. L'angle θ (angle de Bragg) détermine l'incidence
d'un faisceau parallèle de rayons X sur ces plans réticulaires. Notez que θ est
le complémentaire de l'angle d'incidence usuel en optique. La différence de chemin
optique entre les deux rayons lumineux particuliers représentés vaut
AC + CB = 2 d sinθ. Ils interfèrent de manière
constructive lorsque la différence de marche est égale à un nombre entier p de
longueur d'onde. C'est la loi de Bragg :
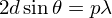 .
.
2. Réseau cristallin et réseau réciproque
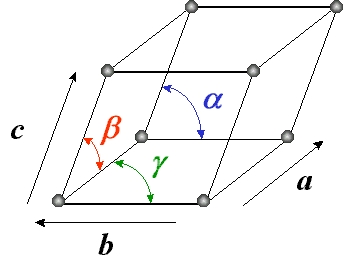
Une maille élémentaire d'un cristal est déterminée par un trièdre formé par trois vecteurs de base a , b , c, faisant entre eux les angles α, β, γ (figure 4). Le pavage des nœuds dans l'espace est représenté par les vecteurs rangées définis par n = u a + v b + w c (u, v et w étant des entiers). À ce réseau direct correspond un réseau réciproque : les vecteurs a* ; b* ; c* tels que a . a* = 1, b . b* = 1, c . c* = 1, a . b* = 0, a . c* = 0, b . a* = 0, b . c* = 0, c . a* = 0, c . b* = 0. De la même manière, les vecteurs rangées du réseau réciproque sont : n* = h a* + k b* + l c* (h, k et l étant des entiers, appelés indices de Miller). En conséquence, un vecteur rangée du réseau réciproque est normal à un plan réticulaire du réseau direct.
Les différents vecteurs des deux réseaux sont représentés figure 5 pour le cas particulier d'un système hexagonal (a=b≠c et α=β=90° et γ=120°). On peut vérifier par exemple que le vecteur a* est perpendiculaire au plan réticulaire (b,c).
Figure 4. Maille cristalline (a, b, c, α, β, γ) |
3. Conditions de Laue
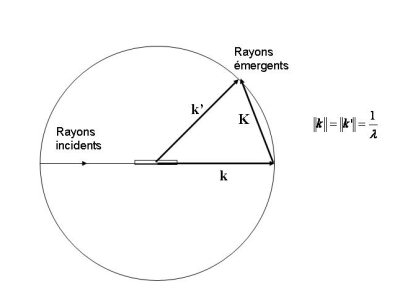
Dans le cas général, on détermine un rayon incident arrivant sur un nœud par son vecteur d'onde k (de norme 1/λ). Le rayon diffusé par ce nœud dans la direction d'observation (vecteur unitaire u) a un vecteur d'onde k' = ‖ k ‖ u. Comme l'interaction entre un photon X et la particule du nœud est élastique, les photons diffusés sont de même énergie que les photons incidents et les vecteurs d'onde k' et k ont la même norme. Le vecteur de diffusion est défini par K = k' - k.
La différence de chemin optique entre deux rayons X émergents après diffusion sur deux nœuds différents localisés en r1 et r2 est égale à K.(r2 – r1). En remarquant que tous les vecteurs qui ont des nœuds aux deux extrémités r1 et r2 constituent justement l'ensemble des vecteurs n du réseau direct, on traduit la condition d'interférences constructives en écrivant que le produit scalaire K . n est un entier.
Autrement dit, il faut que Ksoit un vecteur n* du réseau réciproque : K= h a* + k b* + l c*.
C'est ce qu'expriment les conditions de diffraction de Laue :
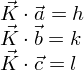
Expérimentalement, la position des pics de diffraction observés nous permet de déterminer les vecteurs du réseau réciproque et donc de décrire la maille cristalline.
4. Analyse de l'intensité des taches de diffraction
L'intensité du signal lumineux diffracté est importante à analyser. En effet, elle dépend de la nature des atomes et de leurs positions suivant le facteur de structure :
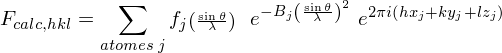
avec xj, yj, zj, les coordonnées de l'atome j dans la maille, fj(sinθ/λ), le facteur de forme de l'atome j et Bj le facteur d'agitation thermique. Cette dernière réduit la cohérence de diffraction entre atomes équivalents dans des mailles différentes. Le facteur fj(sinθ/λ) varie en fonction de l'angle de Bragg θ ; il est égal au numéro atomique Z de l'atome lorsque le faisceau de rayons X n'est pas dévié (θ = 0), car l'ensemble du cortège électronique de l'atome participe à la diffraction. Quand θ augmente, il diminue, du fait de la perte de cohérence entre les ondes diffusées par différentes portions de l'atome. Pour chaque élément chimique, la variation de la fonction f(sinθ/λ) est modélisée par une superposition de quatre exponentielles :
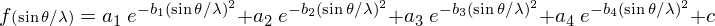
dont les paramètres ai, bi et c sont tabulés.
L'intensité mesurée est proportionnelle au carré du module du facteur de structure et permet de déterminer la nature atomique des éléments chimiques et leur position dans la maille ; il est donc possible de caractériser entièrement le motif cristallin.
Les techniques de diffraction des rayons X
Nature de l'échantillon
Nous venons de mettre en place les outils théoriques de description d'un cristal et de ses interactions avec les rayons X. Nous allons maintenant montrer en détail la mise en œuvre expérimentale par deux méthodes différentes, selon la nature de l'échantillon à analyser : soit un monocristal (dimension de l'ordre de 0,1 mm), soit une poudre cristalline (ensemble de cristaux microscopiques). L'exposition d'un monocristal à un faisceau de rayons X produit une image constituée de taches de diffraction bien définies (fig. 6). Les nombreuses orientations des petits cristaux d'une poudre produisent un très grand nombre de taches groupées en cercles concentriques autour du point θ = 0, du fait de la symétrie de révolution autour de la direction du faisceau incident (fig. 7).
Détermination structurale dans le cas d'un monocristal
Les monocristaux
Un monocristal est composé d'un seul arrangement périodique du même motif. Les cristaux usuels sont constitués d'un amoncellement irrégulier de nombreux monocristaux.
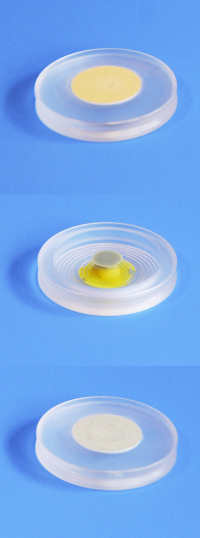
Les cristaux étant des systèmes anisotropes compte tenu de leurs paramètres de maille différents (hormis dans le cas du cubique), ils ont une direction privilégiée pour la propagation de la lumière ; c'est ce qui provoque le phénomène de biréfringence. Par exemple les figures 8 et 9 montrent que la lumière polarisée est modifiée à la traversée d'un cristal biréfringent.
Nous nous servons du phénomène de biréfringence pour faire une première sélection parmi les cristaux synthétisés et déterminer visuellement les monocristaux les plus adaptés à la mesure.
La technique
Le cristal sélectionné est monté sur le diffractomètre, soit à l'aide d'un lasso (fig. 10), soit à l'aide de pâte à modeler pour les plus gros monocristaux (de l'ordre du cm). L'ensemble est fixé sur une tête goniométrique, ce qui va permettre de faire tourner le cristal dans les 3 dimensions et ainsi faire varier l'angle θ. Si le cristal est sensible à l'air, on l'insère dans un tube capillaire rempli de sa solution mère. Cela évite tout contact avec l'oxygène et l'humidité de l'air. On peut également envoyer un flux d'azote liquide grâce à une canne de réfrigération pour travailler à la fois à basse température et sous atmosphère inerte (fig. 11).
Figure 10. Monocristal monté sur un lasso
Figure 12. Vue d'ensemble du dispositif
La résolution de structure
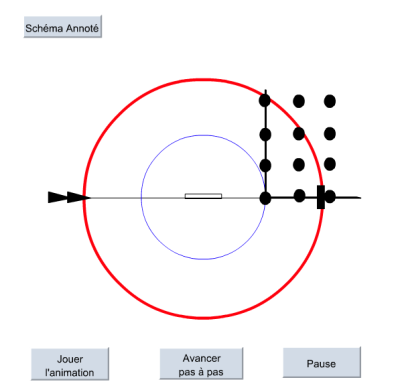
Les taches de diffraction observées correspondent à l'ensemble des directions des vecteurs k' satisfaisant les conditions de Laue (voir la première partie). On définit dans l'espace du réseau réciproque, une sphère de rayon 1/λ centrée sur le cristal, appelée sphère d'Ewald. Selon la direction de diffraction par rapport au réseau du cristal, la sphère d'Ewald intercepte différents nœuds du réseau réciproque. À chaque coïncidence, le vecteur de diffusion K est égal à un vecteur n* du réseau réciproque et il se forme alors une tache de diffraction dans la direction correspondante (fig. 13).
Ceci est illustré par l'animation suivante. On y observe l'apparition successives des taches de diffraction. Pour les six taches observées aux angles de diffraction croissant, on peut remarquer leur ordre d'apparition (1,3,5,2,4,6) et repérer les vecteurs n* correspondants (b*, a*+b*, 2b*, a*+2b*, 3b*, a*+3b*).
Figure 13. Sphère d'Ewald et vecteur diffusion K | Quand un nœud du réseau réciproque croise la sphère d'Ewald, une tache de diffraction apparaît. Voir l'animation « Résolution de structure - formation des taches de diffraction » (animation flash, lecture directe par votre navigateur internet) Télécharger l'animation « Résolution de structure - formation des taches de diffraction » (17,3 ko) |
Le traitement numérique des positions observées des taches de diffraction et de leurs intensités permet de remonter à la structure complète de la molécule. Il faut donc enregistrer un grand nombre de taches pour couvrir au maximum l'ensemble des directions de diffraction.
La distribution des taches de diffraction permet de déterminer la nature du système cristallin (a, b, c, α, β, γ). De l'intensité des différentes taches lumineuses, on déduit le module du facteur de structure Fcalc,hkl (défini au paragraphe « 4. Analyse de l'intensité des taches de diffraction », première partie) ce qui permet de remonter à la structure du motif de diffraction. On fait donc une transformation inverse par rapport à la formule précédente qui exprime Fcalc,hkl comme une somme sur les facteurs fj(sinθ/λ). Toutefois, l'information liée à la phase du nombre complexe Fcalc,hkl est inaccessible en pratique, c'est ce qu'on appelle le problème des phases. Dans le cas de petites molécules, la quantité d'informations mesurées (intensité et position des taches) est suffisante pour s'affranchir de ce problème via des calculs directs ou la méthode de Patterson. Ces modes de traitements permettent d'associer aux figures de diffraction observées, la nature des atomes présents dans la maille et leurs positions respectives.
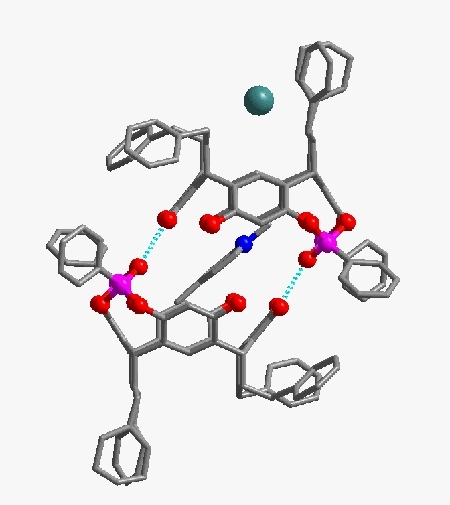
L'exemple ci-après montre comment on peut ainsi dessiner en trois dimensions la structure d'une molécule constituant un motif cristallin.
En gris les atomes de carbone, en rouge l'oxygène, en rose le phosphore, en vert l'iode et en bleu l'azote.
Voir la structure résolue complète de la molécule (image animée gif, lecture directe par votre navigateur internet, 4,3 Mo)
auteur : S. Harthong, travaux de thèse
Il faut alors avoir un avis critique sur la qualité de la mesure en comparant
les facteurs de structure observés (FO) et calculés
(FC). On cherche à minimiser les écarts
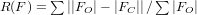 , et
, et
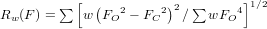 qui doivent
atteindre environ 5 % et maximiser un facteur de qualité d'adéquation
(« Goodness of Fit », noté S), qui doit être le plus proche
de 1.
qui doivent
atteindre environ 5 % et maximiser un facteur de qualité d'adéquation
(« Goodness of Fit », noté S), qui doit être le plus proche
de 1.
Il est bien entendu toujours nécessaire de garder un sens « chimique » pour discuter la vraisemblance des agencements de la structure déterminée.
En résumé, les étapes de résolution complète d'une structure sont les suivantes :
- Sélectionner un cristal de bonne qualité ;
- Centrer le cristal pour pouvoir explorer toutes les directions de l'espace ;
- Déterminer la maille élémentaire en enregistrant environ 10 images ;
- Acquérir les données complètes ;
- Traiter numériquement les mesures ;
- Générer le fichier des informations cristallines (Crystallographic Informations File, appelé fichier CIF).
L'ensemble du traitement de la mesure est automatisé et réalisable à l'aide d'un ordinateur classique, comme cela est décrit dans le film : « Résolution complète d'une structure, exemple de la molécule 3,4-diiodo-vératrole » (vidéo format wmv, 58 Mo, 14 min). La résolution commence en utilisant une hypothèse de travail forte : la formule brute ; et se poursuit par affinements successifs pour ajuster le plus possible la structure obtenue à la mesure effectuée.
L'informatique a permis de considérablement optimiser cette technique. Là où il y a 40 ans il fallait un an pour déterminer une structure relativement simple (une dizaine d'atomes), nous pouvons aujourd'hui résoudre une structure par jour pour des molécules de plusieurs dizaines atomes. Les structures plus complexes comme les protéines nécessitent encore un travail plus approfondi et des diffractomètres présentant certaines spécificités.
La diffraction sur poudre
Si l'échantillon n'est pas monocristallin, on utilise une autre technique qui est la diffraction sur poudre. On observe des cercles concentriques au lieu des taches de diffractions (fig. 7).
Cette technique permet une analyse rapide et non destructive d'un mélange de phases cristallines. Elle est donc très largement utilisée dans de nombreux domaines tels que la minéralogie, la biologie, l'archéologie, la pharmacologie, …
Poudres cristallines
Une poudre est constituée de microcristaux présentant idéalement toutes les orientations cristallines possibles. Il en résulte que l'espace réciproque observé pour un monocristal est projeté selon une seule dimension. L'image de diffraction d'une poudre formée d'une phase cristalline est constituée de cercles spécifiques de la phase. Un diffractogramme (exemples fig. 20) peut donc être considéré comme une empreinte digitale d'une phase cristalline.
Figure 17. Échantillons sous atmosphère inerte |
Diffractomètre sur poudre
Figure 18. Diffractomètre sur poudre | Figure 19. Zoom autour du détecteur |
Dans ce cas, l'échantillon reste fixe et le balayage en angle θ est effectué grâce aux mouvements de la source et du détecteur autour de l'échantillon.
Diffractogrammes, identification de phases et autres applications
Identification de phases
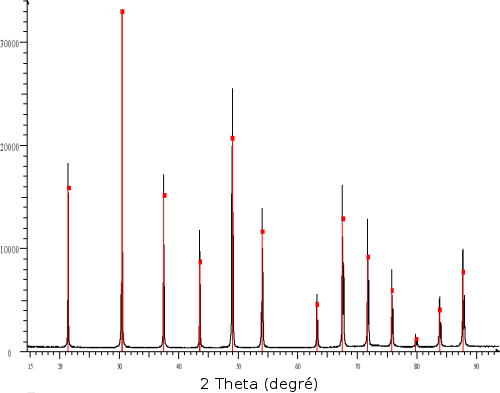
C'est l'application la plus courante de la diffraction des rayons X sur poudre. Une fois le diagramme obtenu, on compare les positions et les intensités des pics observés avec ceux de la base de données PDF (Powder Diffraction File) de l'ICDD (International Centre for Diffraction Data) qui contient plus de 600.000 diagrammes de référence. On peut ainsi rapidement vérifier un résultat de synthèse (bonne phase cristalline, présence d'impuretés,…) ou confirmer que l'on a obtenu un nouveau composé.
(a) En noir la mesure et en rouge l'indexation par le composé de référence LaB6 qui permet d'identifier tous les pics
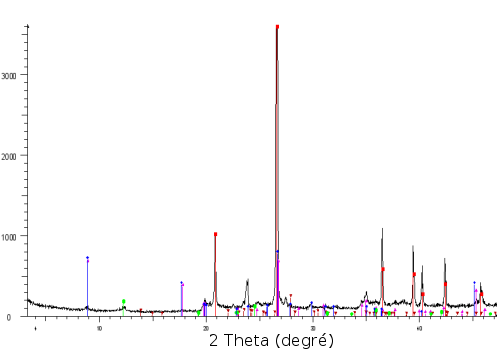
(b) En noir la mesure et en couleur l'association de plusieurs diagrammes de référence (rouge : quartz SiO2 ; violet : Muscovite (K,Na)(Al,Mg,Fe)2(Si3.1Al0.9)10(OH)2 ; bleu : Illite (K,H3O)Al2Si2Al10(OH)2 ; marron : albite NaAlSi3O8 ; vert : lizardite (Al,Mg)3((Si,Fe)2O5(OH)4)
Taux de cristallinité
Les matériaux polymères sont en général des matériaux semi-cristallins, c'est-à-dire qu'ils présentent sur leur diagramme des pics ainsi qu'un signal large correspondant au matériau amorphe. Le rapport d'intensité entre ces deux signaux permet de remonter au taux de cristallinité du polymère.
Étude des paramètres de maille
La position des pics observés est uniquement reliée aux paramètres de maille de la phase cristalline. Il est alors possible de suivre l'évolution de la phase en fonction de divers paramètres tels que la pression ou la température ou encore de caractériser une transition de phase.
Taille des cristallites et micro-déformations
La largeur d'une raie de diffraction provient de facteurs instrumentaux et de caractéristiques physiques de la poudre. On peut ainsi remonter à la taille moyenne des cristallites et à leurs micro-contraintes.
Résolution et affinement de structure
La résolution et l'affinement structural ab initio est également possible à partir d'une poudre mais beaucoup plus délicate et limitée que pour un monocristal à cause du recouvrement des pics de diffraction.
Autres applications
Parmi les autres techniques utilisant la diffraction des rayons X on peut citer la réflectométrie pour l'étude des épaisseurs de couches, les mesures de texture pour mesurer l'orientation préférentielle d'un échantillon ou encore la diffraction des rayons X aux petits angles (SAXS) qui permet des études sur les nano et micro-composés.
Conclusion
La diffraction des rayons X est une technique très puissante car elle permet de déterminer les positions des atomes dans un cristal, mais elle nécessite l'obtention de monocristaux. À l'heure actuelle, la technique Riedvelt se développe pour résoudre des structures à partir de poudres cristallines. Elle n'est pas encore utilisable pour la résolution de grosses structures (plus de dix atomes). Toutefois, tout cela ne s'applique qu'aux composés cristallins. Aussi, des techniques de résolution à partir de poudre amorphe par résonance magnétique nucléaire (RMN) sont l'objet de recherches mais nécessitent encore l'utilisation des paramètres mesurés par diffraction des rayons X.
Pour en savoir plus sur la résonance magnétique nucléaire et ses applications, vous pouvez voir ou revoir sur CultureSciences-Physique la conférence « Hautes performances en RMN et applications » de Lyndon Emsley, chercheur au Centre de RMN à Très Hauts Champs de l'Université de Lyon.
Contacts
Créé en 1976, le Centre de Diffractométrie Henri Longchambon, Université Claude Bernard Lyon I est un laboratoire de service. Il met à la disposition des laboratoires, universitaires ou extérieurs, deux équipements de diffraction des rayons X : un diffractomètre pour monocristaux et un diffractomètre pour poudres. Pour plus de renseignements vous pouvez consulter son site web : http://cdalpha.univ-lyon1.fr/.
Chrostophe Aronica propose entre autres une visite du laboratoire de chimie de l'École Normale Supérieure de Lyon sur ses pages professionnelles : http://perso.ens-lyon.fr/christophe.aronica/.
Pour citer cet article :
Diffraction des rayons X - Techniques et études des structures cristallines, Christophe Aronica, Erwann Jeanneau, octobre 2009. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Diffraction-rayons-X-techniques-determination-structure.xml