Activer le mode zen
Ressource au format PDF
Mots-clés
- intensité du courant
- fil électrique
- effet Joule
- loi de Planck
- résistance
- coefficient de rayonnement
Classification
L'électricité de la maison : section des fils
18/11/2004
Résumé
Quel est le lien entre la section des fils électriques et la puissance des appareils auxquels ils sont branchés ? Une gaine de fil électrique peut-elle être parfaitement isolante thermiquement ? Que se passe-t-il si la section des fils n'est pas adaptée ? Cet article répond simplement à ces quelques questions.
Table des matières
- Première réponse qualitative
- Section de fil correspondant à une puissance donnée
- Puissance dissipée par effet Joule
- Quelle section choisir pour que la chaleur évacuée à la surface du fil soit suffisante pour compenser la chaleur libérée par effet Joule ?
- Analyse qualitative de l'évolution de la température du fil
- Ordre de grandeur de la section minimale de fil correspondant à une puissance donnée
- Conclusion
Pourquoi faut-il des fils de section plus importante pour des appareils de plus forte puissance ?
Première réponse qualitative
Il est facile de donner une première réponse « avec les mains »... La résistance des fils est inversement proportionnelle à la section du fil : plus le fil est gros, plus sa résistance R, et donc la chaleur dégagée par effet Joule pour une intensité donnée, est faible.
Un appareil de plus forte puissance va correspondre à une plus forte intensité, donc, pour que la chaleur dégagée par effet Joule ne soit pas trop forte, il faut diminuer R, c'est-à-dire augmenter la section du fil.
On peut se demander toutefois s'il est possible d'aller plus loin et de calculer la section du fil correspondant à une puissance donnée...
Section de fil correspondant à une puissance donnée
Puissance dissipée par effet Joule
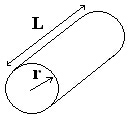
Pour un fil cylindrique de rayon r, de longueur L, de résistivité ρ (ρ = 1,724 × 10-8 Ω.m dans le cas du cuivre) parcouru par une intensité efficace I, on a :
PJoule (puissance thermique produite par effet Joule) = R I2 (R= résistance du fil) = ρ L/(π r2) I2
Si l'appareil branché sur ce fil consomme une puissance efficace P, cette puissance est reliée à l'intensité et à la tension efficaces I et U via la relation :
P = k U I (k < 1) avec k = 1 pour un récepteur passif soit
PJoule = ρ L/(π r2) P2/(k2U2)
Cette puissance dégagée va faire augmenter la température du fil.
Si celui-ci était "parfaitement" isolé thermiquement, le processus continuerait jusqu'à la fonte du fil...
On peut montrer que, la capacité thermique du cuivre étant de 3,9 × 102 J/kg/K et sa masse volumique de 8,9 × 103 kg/m3, 10 min de fonctionnement parfaitement isolé pour alimenter un récepteur passif d'1 kW entraînerait une hausse de température du fil d'une soixantaine de degrés!
Heureusement, ceci ne se produit pas car la chaleur du fil s'évacue...
La gaine du fil doit donc idéalement isoler le fil du point de vue électrique, mais ne doit pas être un "trop bon" isolant thermique. La gaine doit par contre résister à l'élévation de température engendrée par l'échauffement du fil.
Quelle section choisir pour que la chaleur évacuée à la surface du fil soit suffisante pour compenser la chaleur libérée par effet Joule ?
On va choisir le modèle simple d'un fil nu (non gainé) en contact avec de l'air immobile. On verra que ce modèle permet d'ores et déjà des calculs qualitatifs intéressants. On a :
Pévacuée ∝ (Tfil - Textérieur) × Surface de contact entre le fil et l'air
(la température à l'intérieur du fil, dans ce modèle, est considérée comme homogène. Pour une section de l'ordre du millimètre carré, cette approximation est raisonnable)
soit
Pévacuée ∝ (Tfil - Textérieur) × 2 π r L
Le coefficient de proportionnalité est appelé "coefficient de rayonnement" en l'absence de convection au voisinage du fil. Il est déduit de la loi de Planck, et est de l'ordre de la dizaine dans notre cas.
Dans la pratique, le phénomène de convection si le fil est dans un endroit ventilé modifie le coefficient de proportionalité, bien qu'il ne modifie pas le reste de la relation. De plus, le fil n'est que rarement nu. Faire intervenir sa gaine plastique exige de connaître sa forme exacte et sa nature, qui varie suivant les fils (gaine simple entourant un seul fil, gaine entourant un ensemble de plusieurs fils, gaines multiples, etc.)...
La variété des situations est trop grande pour espérer faire ici un calcul quantitatif général, seuls des calculs sur chaque cas particulier sont possibles... On peut néanmoins faire des raisonnements qualitatifs ou semi-quantitatifs intéressants, et c'est ce que nous allons faire dans la suite de ce paragraphe. Pour l'essentiel, les résultats obtenus sur un fil nu donnent déjà une bonne idée de la situation...
Analyse qualitative de l'évolution de la température du fil
On voit que la puissance dissipée par effet Joule ne dépend pas de la température du fil, tandis que la puissance évacuée est d'autant plus grande que l'écart de température entre le fil et l'extérieur est importante. Par conséquent, la température du fil va d'abord augmenter (lors de cette phase, Pévacuée < PJoule) avant d'atteindre une valeur limite pour laquelle Pévacuée = PJoule, soit, en ordre de grandeur (k est de l'ordre de 1) et en simplifiant par L de part et d'autre de l'équation:
ρ/r2 P2/U2 = Coefficient de rayonnement × (Tfil - Textérieur) r
ou P2/r3 ∝ (Tfil - Textérieur)
Si la température d'équilibre est supérieure à la température de fusion des composants en contact avec le fil, il y a danger. Dans le cas réaliste d'un fil gainé, on veut éviter la fonte de la gaine... On veut aussi, bien évidemment, éviter que l'échauffement des fils n'endommage les objets avec lesquels ils sont en contact ou créent un incendie. La température d'équilibre du fil doit donc être sensiblement inférieure à une centaine de degrés. On voit que la température limite atteinte ne dépend pas de la longueur du fil (ce dont on pouvait se douter) mais de sa section. Lorsque la puissance de l'appareil augmente, on voit que, pour que la température du fil ne dépasse pas la valeur maximale autorisée, il faut augmenter la section du fil.
Courts-circuits et fusibles :
un des risques importants d'incendie d'origine électrique dans une maison est le court-circuit. Dans le cas d'un court-circuit, l'intensité traversant les fils devient subitement très élevée, et, par suite, l'échauffement des fils augmente fortement. Le but des fusibles est justement de fondre et de couper ainsi le circuit avant que la température des fils électriques ne devienne dangereuse.
Ordre de grandeur de la section minimale de fil correspondant à une puissance donnée
En ordre de grandeur, on peut écrire :
ρ/r2 P2/U2 = Coefficient de rayonnement × (Tfil - Textérieur) r
ρ ∼ 10-8 Ω.m
P ∼ 103 W
U ∼ 102 V
Coefficient de rayonnement : de l'ordre de 10 W.m-2.K-1
(Tfil - Textérieur) est de l'ordre de 10 K pour que les fils et leurs gaines plastiques ne fondent pas.
On en déduit que r3 ∼ 10-8 m3 ce qui nous donne r de l'ordre du millimètre.
Ceci correspond bien aux normes en vigueur : je trouve ainsi, par exemple, un fil double de section de 1 mm2 correspondant à une puissance maximale de 1,3 à 1,5 × 103 W, un fil rigide de section de 4 mm2 correspondant à une puissance de 4 × 103 W, etc.
On ne peut pas faire de calcul simple de proportionnalité entre P et la section à la puissance 3/4, comme les expressions ci-dessus pourraient nous y inciter du fait la variété des fils et de leur gaines (gaine simple, gaine contenant plusieurs fils, matériau de la gaine, fil torsadé, etc.)...
Conclusion
Même sans utiliser des outils mathématiques compliqués, il est possible de comprendre l'importance de la section des fils électriques utilisés dans la maison. Ainsi, lorsqu'on refait l'électricité, il faut se préoccuper non seulement des branchements, mais aussi des puissances maximales indiqués sur les fils que l'on achète... Des "économies" sur la section des fils peuvent avoir des conséquences dangereuse : une gaine qui fond, c'est l'isolation électrique du fil qui disparait, et donc un risque de court-circuit ou d'électrocution...
Pour citer cet article :
L'électricité de la maison : section des fils, Gabrielle Bonnet, novembre 2004. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/CalibreFils.xml