Démonstration de l'isochronisme des grandes oscillations dans le cas du pendule cycloïdal de Huygens

retour à l'article principal

Démonstration

La démonstration que l'on trouve dans les livres est souvent plus géométrique mais faire la démonstration complète de cette façon requiert des connaissances de mathématiques sur les développantes et développées que tout le monde ne possède pas... Voilà pourquoi nous avons choisi ici une démonstration analytique qui nous permet de maîtriser la totalité de la démonstration.

• Equation de la gorge cycloïdale :

On va représenter la cycloïde donnant le profil de la gorge du pendule dans un repère (x,z) tel que le point d'attache du fil soit à x = z = 0.

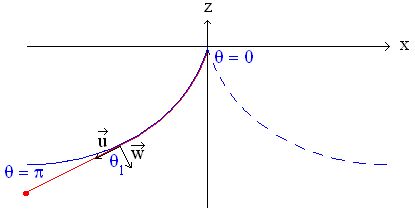
dans ce cas, l'équation du profil de la gorge de gauche sur le schéma est :

x = a (- θ + sin θ)

z = a (cos θ - 1)

on choisit un pendule tel que, lorsqu'il est totalement enroulé sur la gorge, la masse se trouve exactement au niveau du minimum de la cycloïde, le point θ = π, x = - a π, z = - 2 a.

On veut montrer que, quelle que soit la position de départ à partir de laquelle on le lâche, le pendule arrive à sa position d'équilibre (x = 0) dans le même temps.

• Courbe décrite par l'extrémité du pendule

Calculons la longueur de fil en contact avec le profil lorsque le pendule est enroulé sur la joue jusqu'au point de la cycloïde pour lequel θ = θ₁
On calcule d'abord l'abscisse curviligne s au point x, z de la cycloïde à partir de l'expression ds/dθ = (dx/dθ² + dz/dθ²)^1/2.
On obtient (le calcul est laissé au lecteur) ds/dθ = 2 a sin θ/2 soit s(θ₁) = ∫₀^θ₁ ds/dθ = 4 a (1 - cos θ₁/2)

lorsque θ₁ = π, tout le fil est enroulé et s(π) = 4 a donc la longueur totale du fil est 4 a.
La longeur du fil enroulée est 4 a (1 - cos θ₁/2), la longueur libre est par conséquent l_libre = 4 a cos θ₁/2.
La direction du fil libre est la tangente à la cycloïde au point θ = θ₁ qui est donnée par la direction du vecteur (dx/dθ , dz/dθ) soit u = (- sin θ₁/2 , - cos θ₁/2)

Les coordonnées de la masse, à l'extrémité du fil sont donc, lorsque le paramètre est θ :
X = x(θ) + l_libre × (- sinθ/2)
Z = z(θ) + l_libre × (- cosθ/2)

ce qui donne :

• Période du pendule

Soit V la vitesse de la masse du pendule, on a V = (dX/dt,dZ/dt) = - 2 a cosθ/2 θ'(t) w où w = (cos θ/2, - sin θ/2) est perpendiculaire à u (direction du fil) donc à la tension T du fil.

Le théorème de l'énergie mécanique donne :
1/2 V² + g Z = constante
(la tension du fil, perpendiculaire à la vitesse, ne travaille pas)
soit
2 a² cos²(θ/2) θ'² + g Z = g Z₀
(Z₀ est l'altitude à laquelle on lâche le pendule sans vitesse initiale)
soit, moyennant un calcul peu agréable mais sans difficulté :
- Z'² (Z/a + 2)^-1 = g (Z₀ - Z) ou Z' = - (g/a (Z₀ - Z) (Z + 4 a))^1/2

La période du pendule vaut T = 4 ∫_{1/4 de période} dt = 4 ∫_{1/4 de période} dZ/Z' = 4 ∫_Z0^{-4 a} dZ/Z'
ce qui donne, grâce au changement de variable Y =(Z + 4 a)/(Z₀ + 4 a)

T = 4 ∫₀¹ (g/a (1 - Y) Y)^-1/2 dY
qui est indépendant de Z₀, donc le pendule est bien isochrone.

N.B.: la période est la même que celle du pendule ordinaire pour des oscillations infinitésimales, soit T = 2π (4 a/g)^1/2 (4 a est la longueur du fil du pendule cycloïdal).

retour à l'article principal