Plus vite que la lumière : effet Cherenkov

L'effet Cherenkov, découvert et interprété par le physicien russe Pavel Cherenkov, lui a valu le prix Nobel en 1958. L'effet Cherenkov se produit lorsqu'une particule se déplace plus vite que la vitesse de la lumière dans le milieu considéré. Elle ne va toutefois pas plus vite que la vitesse de la lumière dans le vide, il n'y a donc rien de contradictoire avec la théorie de la relativité. Si v est la vitesse de la particule, et n l'indice du milieu, on a :

$\frac{c}{n}\mathrm{(vitesse\; de\; la\; lumière)}\le v<c$

Aller « plus vite que la lumière » est, tout comme « aller plus vite que le son », accompagné de phénomènes particuliers, c'est à ces phénomènes qu'on a donné le nom d'« effet Cherenkov ». Lorsqu'un avion atteint puis dépasse la vitesse du son : il se produit un « bang » sonore caractéristique, on dit que l'avion « passe le mur du son ». Lorsqu'il s'agit de dépasser la vitesse de la lumière, il y a là aussi des phénomènes singuliers, lumineux et non plus sonores cette fois. Une particule qui atteint la vitesse de la lumière dans le milieu dans lequel elle se déplace émet une lumière intense, de couleur bleue. Au-delà de la vitesse de la lumière, cette particule constitue la pointe d'un cône lumineux de couleur bleue dont l'angle au sommet dépend de la vitesse de la particule.

Où observe-t'on l'effet Cherenkov ?

Photo CEA

Figure 1. "Piscine" de centrale nucléaire, dont la couleur bleue est due à l'effet Cherenkov (Photo CEA)

La couleur bleue dans la piscine des centrales nucléaires est due à l'effet Cherenkov, des particules sont en effet émises à très grandes vitesses lors des désintégrations radioactives qui se produisent dans le réacteur avant d'être ralenties par l'eau.

Les astronautes ont pu eux aussi observer des éclairs bleus dans leurs yeux, dus à l'effet Cherenkov : dans l'humeur aqueuse de l'oeil, il est possible à des particules cosmiques extrêmement rapides d'aller plus vite que la vitesse de la lumière dans ce milieu, créant ainsi un effet Cherenkov. On n'observe pas cet effet à la surface du globe car les particules cosmiques sont ralenties ou absorbées par l'atmosphère avant d'arriver au sol.

L'effet Cherenkov est très utilisé pour déterminer la vitesse de particules très rapides en mesurant l'angle du cône lumineux émis par les particules. Le détecteur super-Kamiokande au Japon, en particulier, utilise l'effet Cherenkov. Enfin, l'effet Cherenkov est même utilisé en médecine !...

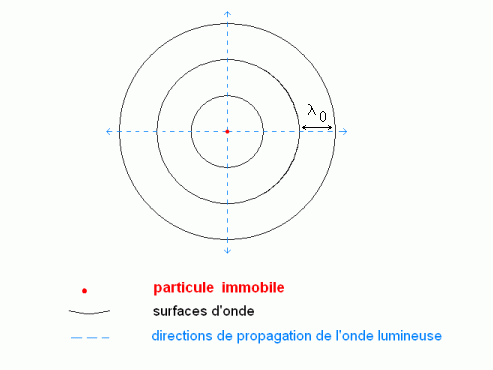
Lorsqu'une particule immobile émet de la lumière (on suppose qu'elle rayonne de façon isotrope) de longueur d'onde λ₀ dans un milieu d'indice n, les surfaces d'onde à un instant donné (surfaces sur lesquelles, à cet instant, l'amplitude de l'onde est maximale) sont des sphères concentriques, centrées sur la particule émettrice, et séparées par la distance λ₀.

L'onde se déplaçant à la vitesse de la lumière $v_1=\frac{c}{n}$, le rayon de ces sphères s'accroît de la longueur v_l t pendant la durée t. En outre, l'onde a une période temporelle T donc tout se passe comme si les surfaces d'onde, ces sphères concentriques, étaient "émises" toutes les périodes $T=\frac{{\lambda }_0}{v_1}$. Cette période est de l'ordre de 10^-15s.

Gabrielle Bonnet

Figure 2. Particule immobile émettant à la longueur d'onde \( \lambda_0 \)

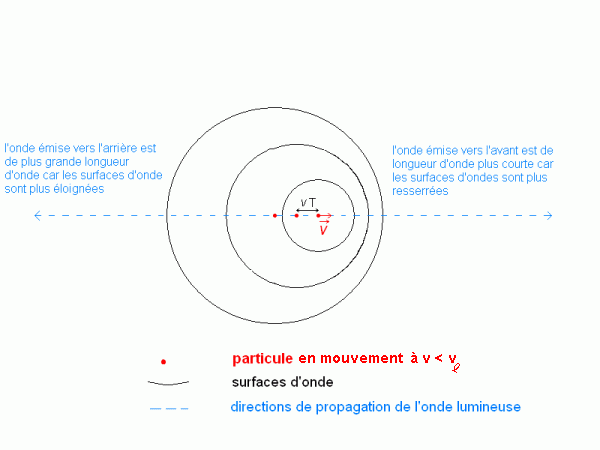
Lorsque la particule est en mouvement à la vitessev, les surfaces d'ondes sont là encore des sphères, qui s'élargissent de façon isotrope, centrées sur le point en lequel elles ont été "émises". Toutefois, cette fois-ci, comme la particule se déplace, les centres des diverses surfaces d'onde sont décalés.

Gabrielle Bonnet

On voit que la longueur d'onde de l'onde dépend de la direction suivant laquelle on l'observe. On a ici représenté seulement deux directions d'observations, correspondant aux valeurs extrêmes de la longueur d'onde, mais il est évident que l'on peut observer l'onde lumineuse émise dans toutes les directions de l'espace.

Figure 3. Particule en mouvement à une vitesse inférieure à celle de la lumière

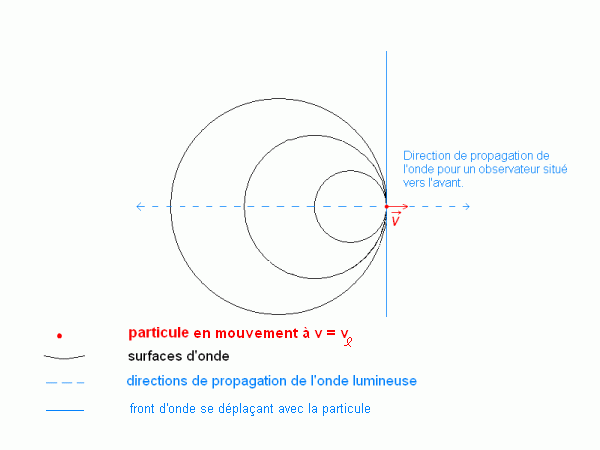
Que se passe-t'il lorsqu'on atteint la vitesse de la lumière dans le milieu? On voit qu'alors, vers l'avant, la longueur d'onde calculée précédemment : $\lambda ={\lambda }_0(1-\frac{v}{v_1})$, qui est aussi la distance entre deux surfaces d'ondes successives, vaut 0 (v = v_l). La particule "rattrape" l'onde qu'elle émet : ainsi, toutes les sphères sont concourantes au même point (ce point est la position de la particule à cet instant). L'énergie lumineuse émise vers l'avant est donc concentrée sur le plan perpendiculaire à la trajectoire de la particule et passant par sa position à cet instant et on a un "flash" lumineux.

Gabrielle Bonnet

Figure 4. Particule se déplaçant à la vitesse de la lumière

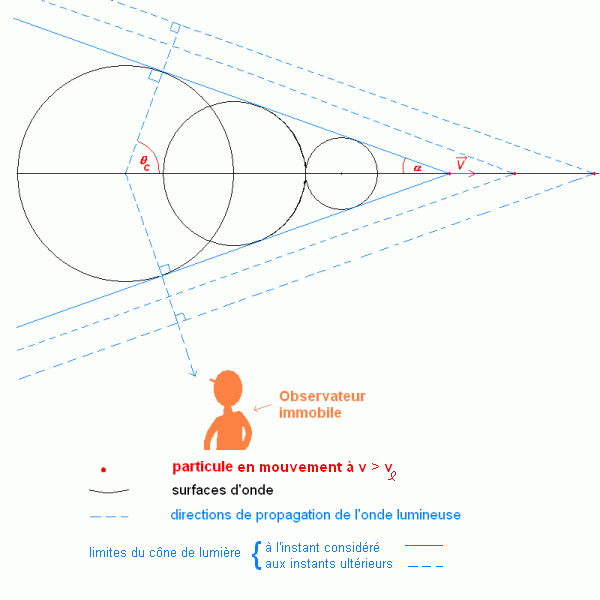
Lorsque la particule dépasse la vitesse de la lumière dans le milieu dans lequel elle se déplace, elle va plus vite que les surfaces d'onde qu'elle "émet" et ces-dernières se retrouvent "derrière" la particule. Elles sont toutes incluses dans un cône dont le sommet est la particule en mouvement. Le demi-angle au sommet de ce cône sera noté α (voir dessin ci-dessous).

On peut calculer α en écrivant, dans le triangle rectangle dont un des sommets est la position de la particule à l'instant considéré et les côtés une des génératrices du cône (en bleu sur le dessin), la trajectoire de la particule (en noir sur le dessin, c'est l'axe du cône), et le rayon d'une des surfaces d'onde :

soit, si la surface d'onde considérée a été émise t secondes plus tôt,

(le rayon des sphères croît à la vitesse v_l)

On constate que, plus l'indice ou la vitesse sont grands, et plus α est petit, sans toutefois atteindre 0 : la valeur minimale de l'angle α correspond en effet, pour un indice donné, à v = c soit $sin\alpha =\frac{1}{n}$. La valeur maximale de α vaut 90°, quel que soit n, et est atteinte lorsque la particule se déplace à la vitesse de la lumière dans le milieu.

Gabrielle Bonnet

Figure 5. Particule dépassant la vitesse de la lumière

Nous voyons que l’effet Cherenkov est bien dû au dépassement de la vitesse de la lumière par une particule matérielle chargée, provoquant un phénomène de « flash » par concentration locale de l’onde lumineuse, analogue au « mur du son » dans le domaine acoustique. Il n’y a aucune contradiction avec le fait que la vitesse d’une particule relativiste reste toujours inférieure à la vitesse de la lumière dans le vide. L’effet Cherenkov est possible parce que la lumière se propage dans le milieu à une vitesse inférieure à sa vitesse c de propagation dans le vide.

Article précédent : « Relativité et vitesse de la lumière ».

Dossier : « La vitesse de la lumière ».

Article suivant : « Vitesse superluminique en astronomie ».