Les planètes extrasolaires

L'idée qu'il existe peut-être d'autres mondes "semblables au nôtre" est très ancienne : elle remonte à l'antiquité. Toutefois, elle a souvent valu à ses défenseurs (Epicure, Giordano Bruno, Galilée...) des démêlés avec les tenants des courants de pensée majoritaires de leur époque. Ces premières conjectures n'étaient alors que des hypothèses invérifiables : ce n'est que presque deux millénaires plus tard qu'eurent lieu les premières tentatives pour obtenir des preuves expérimentales. Celles-ci débutèrent avec Huyghens qui fut le premier à essayer de détecter, en 1689, des planètes en-dehors de notre système solaire. Comme les instruments de l'époque n'étaient pas assez puissants, ces tentatives furent abandonnées et il faudra attendre 1992 pour découvrir enfin la première planète extrasolaire.

Contrairement à ce à quoi on aurait pu s'attendre, cette planète ne gravite pas autour d'une étoile de la séquence principale* mais d'un pulsar*, PSR1257+12. Elle n'est pas la seule dans son cas : deux autres planètes ont par la suite été découvertes autour du même pulsar, puis d'autres planètes encore autour d'un deuxième pulsar. Bien que les trois planètes gravitant autour de PSR1257+12 aient des masses du même ordre que celle de la Terre (comprises entre 0,015 et 3,4 fois la masse de la Terre), il serait difficile de les considérer comme des "jumelles de la Terre" : leur astre central et notre Soleil sont trop dissemblables pour cela.

Il fallut attendre 1995 pour découvrir la première planète extrasolaire en orbite autour d'une étoile de la séquence principale, l'étoile 51 Pégase. Il s'agit d'une planète géante dont la masse est d'environ la moitié de celle de Jupiter. Elle gravite très près de son étoile : à un vingtième de la distance Terre-Soleil seulement et décrit son orbite en 4 jours!

Les découvertes se sont succédées par la suite (une centaine de planètes extrasolaires mises en évidence jusqu'à ce jour), et à l'heure actuelle, on peut même se faire quelques idées (prudentes encore, car seuls certains types de planètes sont accessibles aux instruments actuels!) de leur répartition dans l'univers : on peut ainsi affirmer qu'à peu près 5% des étoiles de la séquence principale ont une planète géante en orbite à moins de deux unités astronomiques de distance (une unité astronomique, en abrégé u.a., correspond à la distance moyenne entre la Terre et le Soleil, soit 1,50 . 10⁸ km).

Les résultats obtenus ont de nombreuses conséquences scientifiques et philosophiques, et soulèvent un certain nombre de questions auxquelles il a fallu ou faudra répondre, en particulier la position des planètes géantes observées, qui ne correspond pas aux prévisions, ou l'existence de planètes autour de certains pulsars. L'existence d'autres systèmes solaires, avec une ou plusieurs planètes (jusqu'à 3 pour les systèmes détectés à ce jour) est désormais prouvée. Cependant, aucune planète semblable à la Terre n'a encore été découverte. Il y a à cela une raison très simple : les méthodes actuelles, si elles permettent de détecter les planètes les plus grandes, ne permettent pas de déceler (sauf autour d'un pulsar, nous verrons plus loin pourquoi) des planètes de la taille de la Terre. Ainsi, on ne sait pas si (et si oui, avec quelle fréquence) il existe dans l'univers des planètes qui soient à la fois de la taille de la nôtre et en mouvement autour d'une étoile de la séquence principale. Une taille proche de celle de la Terre ne suffirait d'ailleurs pas à faire d'une telle planète une "jumelle de la nôtre" (c'est-à-dire en particulier une planète abritant la vie) : il lui faudrait aussi une température de surface convenable, et une atmosphère de composition chimique semblable à la nôtre. On espère cependant au cours des 20 ans à venir faire suffisamment de progrès pour pouvoir répondre à ces questions.

C'est la méthode grâce à laquelle la majorité des planètes découvertes jusqu'à ce jour ont pu être détectées. Elle permet de déterminer la période de l'orbite de la planète découverte, ainsi qu'une limite inférieure sur la masse de cette-dernière.

Ordres de grandeur des masses et distances :

Pour un système étoile-planète semblable au système Terre-Soleil, le rapport de la masse de l'étoile sur la masse de la planète, qui est égal au rapport de la masse du Soleil sur la masse de la Terre, est de 3,3 . 10⁵. Par conséquent, si, comme la Terre, la planète décrit une orbite à 1 unité astronomique du centre du système, l'étoile, elle, décrit une orbite de 1/(3,3 . 10⁵) unités astronomiques de rayon, soit 4,5 . 10⁵ m seulement! La période de l'étoile étant forcément la même que celle de la planète, soit ici 365 jours, sa vitesse dans le référentiel du centre d'inertie du système serait alors d'une dizaine de cm/s!

Pour un système étoile-planète semblable au système Jupiter-Soleil, le rapport des masses est de 1,0 . 10³, l'étoile devrait donc décrire en 11,9 ans (durée d'une année Jovienne) une orbite de 7,5 . 10⁵ km de rayon soit une vitesse (dans le référentiel du centre d'inertie du système) de 13m/s à peu près.

Pour la première planète détectée par cette méthode, en 1995 autour de 51 Pégase, la vitesse de l'étoile autour du centre d'inertie du système est de plusieurs dizaines de m/s, c'est-à-dire sensiblement plus que les vitesses précédentes. Ceci explique que cette planète ait été la première détectée.

Depuis lors, la précision s'est améliorée et on détecte des vitesses de l'ordre de 3 m/s (ceci correspondrait à un système semblable au système Soleil-Saturne). A l'avenir, on compte augmenter encore la précision pour arriver, au final, à détecter des planètes de la taille de la Terre.

Gabrielle Bonnet

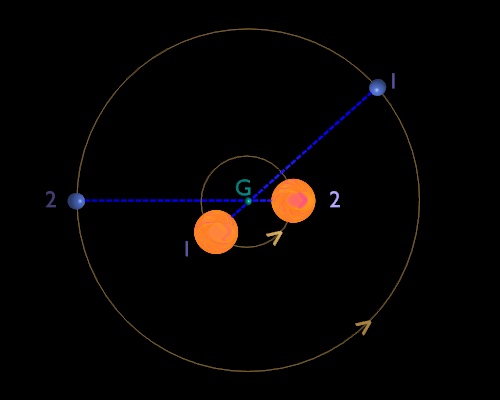
Représentation, en vue de dessus, des orbites de l'étoile et de la planète d'un système comprenant une seule étoile et une seule planète. G est le centre d'inertie du système (le dessin n'est pas à l'échelle!). L'étoile et la planète sont représentées à deux dates différentes (1 et 2).

Mesure de la vitesse radiale des étoiles.

On n'observe pas directement le mouvement de l'étoile, mais on étudie les effets indirects, par effet Doppler*, de ce mouvement sur le spectre de l'étoile.

Une étoile, même dépourvue de planète, est en mouvement par rapport à l'observateur terrestre (cette vitesse peut être de l'ordre de 250km/s!). Lorsque l'étoile possède un cortège planétaire, on ajoute à cette vitesse sa vitesse autour du centre d'inertie du système étoile-planète (au plus quelques dizaines de m/s). La vitesse radiale de l'étoile, c'est-à-dire sa vitesse suivant l'axe Terre-étoile est la seule à pouvoir être déterminée par l'étude des raies spectrales de l'étoile car c'est la seule qui entraine un effet Doppler. Elle est composée d'une vitesse constante (correspondant à la vitesse du système par rapport à l'observateur terrestre), à laquelle s'ajoute une perturbation qui varie de façon périodique. La période de la perturbation donne la période du mouvement de l'étoile, qui est aussi la période du mouvement de la planète, et l'amplitude de la perturbation permet de connaître la valeur de la vitesse de l'étoile sur son orbite, à l'inclinaison i de la normale à l'orbite par rapport à l'axe de visée près (cf schéma) : v_mesurée=v_réelle sin i. Le calcul dans le cas d'une trajectoire circulaire est aisé à faire, et on trouve que la masse m de la planète est reliée à la vitesse réelle v de l'étoile autour de son centre d'inertie, à sa masse M et à sa période T par la relation :

v = (2 π G / T)^1/3 m (M+m)^-2/3 (démonstration en note*)

où G=6,67.10^-11 S.I. est la constante de Newton

(dans le cas général, il suffit d'ajouter (1-e²)^{-1 / 2} dans le membre de droite de l'équation, où e est l'excentricité de l'orbite de la planète)

Si M est très grand devant m, la masse de la planète est donc proportionnelle à la vitesse de l'étoile dans le référentiel du centre d'inertie du système, et comme celle-ci dépend de la vitesse mesurée v_m via v = v_m / sin i, on ne peut déterminer par les mesures que m sin i, qui ne donne qu'une borne inférieure pour la masse véritable et non la valeur exacte de celle-ci.

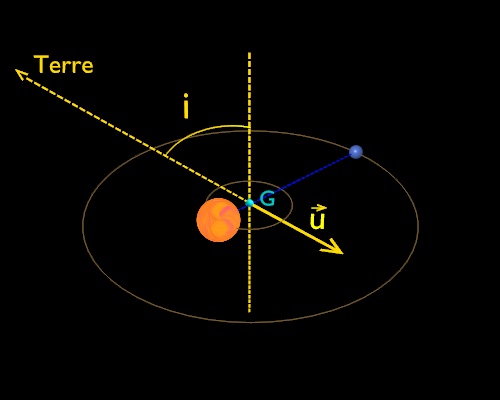
représentation de l'axe de visée et de la trajectoire de l'étoile dans le cas où l'orbite est circulaire. La vitesse radiale mesurée v_mesurée à un instant donné est le produit scalaire v.u et non v_réelle

On rencontre un certain nombre de difficultés lors de la mise en oeuvre de cette méthode, en particulier, comme on n'a accès qu'à la composante radiale du mouvement de l'étoile, on n'a pas assez de données pour déterminer totalement la masse de la planète. De plus, les raies observées sont élargies par différentes causes, ce qui limite la précision des mesures de v donc la détection des planètes.

Effet Doppler :

une onde émise par un objet en mouvement est captée par l'observateur à une fréquence différente de la fréquence d'émission (la fréquence est plus grande si l'objet se rapproche de l'observateur, plus faible dans le cas contraire). Pour les ondes lumineuses émises par des étoiles en mouvement, ceci se traduit par un décalage des raies spectrales.

Démonstration de la formule reliant v et m, masse de la planète :

notations nécessaires dans les calculs intermédiaires :

• r : distance étoile-planète
• r* : distance étoile-centre d'inertie
• v : vitesse de l'étoile dans le référentiel du centre d'inertie du système
• a : accélération de l'étoile dans le référentiel du centre d'inertie du système
• ω : vitesse angulaire de l'étoile, aussi égale à 2 π /T, où T est la période du mouvement
• k : vecteur unitaire dirigé dans le sens étoile-planète

On applique la deuxième loi de Newton à l'étoile : G m M / r²k = M a

En projetant sur l'axe étoile-planète et en simplifiant par M, on obtient : G m = a r²

or r = r* (M+m)/m donc G m³/(M+m)² = a r*², de plus, a= v²/r* donc a r*² = v² r* = v² v/ω = v³ T/(2 π)

On obtient G m³/(M+m)²= v³ T /(2 π) et on trouve donc finalement : v = (2 π G / T)^1/3 m (M+m)^-2/3

La période de rotation propre d'un pulsar milliseconde est de l'ordre d'1 ms. Son rayonnement électromagnétique balaie donc la Terre à ce rythme. Ces signaux sont reçus à intervalles de temps extrêmement réguliers, on a donc une très bonne précision sur la fréquence du pulsar. Si on imagine un pulsar de masse standard (1,35 fois la masse de notre Soleil, par exemple), possédant une planète semblable à la Terre, le rayon de l'orbite du pulsar est alors 3,3 . 10⁵ m environ et sa vitesse est de l'ordre de 7 cm/s. Comme dans le cas d'une étoile de la séquence principale, le mouvement du pulsar autour du centre d'inertie du système entraine un décalage Doppler de la fréquence du signal détecté. Alors qu'un décalage aussi faible ne peut pas être mesuré dans le cas d'étoiles appartenant à la séquence principale, il peut être mesuré dans le cas d'un pulsar. En effet, la très grande stabilité de la rotation du pulsar (la variation de période est de l'ordre de 10^-19 secondes par secondes), permet la détection du décalage relatif (de l'ordre de 10^-10 secondes par seconde) occasionné par le mouvement du pulsar. On a détecté par cette méthode des planètes de masse proche de celle de la Terre, alors qu'elles ne sont pas accessibles par les autres techniques de détection. On obtient ici deux grandeurs : la période de rotation et la masse m de la planète détectée.

Une autre méthode indirecte de détection consiste à repérer la planète en observant son influence sur le mouvement de l'étoile. Ce mouvement est extrêmement réduit : il s'agit de repérer une amplitude de l'ordre de 10^-5 secondes d'arc, ce qui équivaut à observer depuis la Terre un mouvement de l'ampleur d'une pièce de 5 Francs sur Jupiter!

Malgré la difficulté, cette méthode a permis d'obtenir un premier résultat en décembre 2002 : il s'agit d'une étoile de très faible masse (environ 0,3 × la masse du Soleil), très proche de nous (seulement 15 années lumière) et possédant une planète très massive (le rapport de la masse de l'étoile sur la masse de la planète est de l'ordre de 100). Pendant 4 ans la NASA a accumulé les mesures qui ont permis d'étudier le mouvement de cette étoile (ceci revient à observer depuis la Terre une pièce de 2 euros placée sur la Lune) et d'en déduire un certain nombre de caractéristiques de la planète observée.

Une fois de plus, la méthode ne permet pas de déduire toutes les coordonnées d'espace du mouvement, mais seulement leur projection dans un plan perpendiculaire à l'axe de visée. Cependant, en combinant ces résultats avec la mesure par vitesse radiale (qui concerne la composante de la vitesse parallèle à l'axe de visée), on peut éliminer les inconnues géométriques et donner la première masse "exacte" d'une planète extrasolaire : elle est comprise entre 1,9 et 2,4 fois la masse de Jupiter. Certes, l'incertitude sur le résultat est encore importante, mais, pour la première fois on obtient un encadrement (et non la seule limite inférieure) de la masse d'une planète extérieure au système solaire. On espère améliorer la précision des observations (d'ici 3 ou 4 ans environ) et atteindre une précision de 10^-5 secondes d'arc sur la valeur "exacte" des masses d'une majorité des planètes détectées actuellement par vitesse radiale.

On devrait voir diminuer l'éclat de l'étoile lorsqu'une planète passe devant elle... La diminution serait de 1% environ aux yeux d'un observateur lointain si Jupiter passait entre cet observateur et le Soleil, de moins de 0,01% pour une planète comme la Terre. L'atténuation n'est vraiment observable que si la planète passe régulièrement et souvent devant l'étoile : ceci limite l'application aux cas favorables où la planète orbite dans un plan bien orienté par rapport à la ligne de visée, l'idéal étant que le plan de l'orbite contienne la ligne de visée (angle i d'inclinaison nul). En 2000, une planète a été observée par cette technique autour de HD209458. Cette méthode donne la période de l'orbite de la planète, ainsi que son rayon. Comme on sait que l'angle i est très proche de 0, on obtient la masse exacte de la planète. On peut donc évaluer pour la première fois la masse volumique d'une planète extrasolaire. Au moment du passage de la planète devant l'étoile, on peut enregistrer la faible variation de son intensité lumineuse : décroissance progressive, palier et croissance. La dérivée de la courbe de lumière renseigne sur le rayon de la planète.

Une limite évidente de cette méthode est la faible chance que la planète passe, au cours de son mouvement, entre son étoile et nous (pour un observateur lointain, cette probabilité serait de l'ordre de 10^-4 à 10^-7 selon que la planète est la Terre ou Jupiter).

Si une planète passe sur l'axe de visée d'une étoile lointaine, la présence de sa masse dévie la lumière issue de cette étoile, par effet gravitationnel. Cet effet de "lentille gravitationnelle" peut servir à mettre en évidence la présence de certaines planètes extrasolaires très éloignées de leur étoile (à au moins 570 u.a. de distance). Mais l'observation d'une lentille gravitationnelle n'est pas reproductible... Ce qui ne permet aucune confirmation des résultats individuels mais conduit à des études statistiques de la fréquence du phénomène.

Il existe de nombreuses techniques dites "interférométriques". Une de ces techniques consiste à associer plusieurs télescopes, envoyés dans l'espace, et séparés par des distances fixes. Ceci permettrait de gagner énormément en précision. Le gain en résolution angulaire par rapport à un télescope isolé est de l'ordre du rapport entre la distance séparant les télescopes de l'association et le diamètre d'un seul des télescopes ( Δα ≈ λ/ D pour un seul télescope de diamètre D, Δα ≈ λ / d pour des télescopes séparés par la distance d). Par cette méthode, on espère (projet TPF des Etats-Unis, projet ISIS européen) réussir vers 2020 à observer l'image d'une planète semblable à la Terre, au lieu de seulement détecter son effet sur l'étoile. On espère aussi analyser son atmosphère, et déterminer la présence ou non de photosynthèse (donc de vie analogue à la nôtre) : pour cela, il faudra déterminer si l'atmosphère de la planète possède les bonnes proportions d'ozone O₃, de méthane CH₄ et d'eau H₂O.

Ce qui suit ne prétend pas apporter de réponse définitive aux problèmes mais expose un certain nombre d'hypothèses qui ont été avancées.

Les planètes extrasolaires font rêver l'humanité depuis longtemps. Il n'est donc pas étonnant que la presse se soit parfois fait l'écho de nouvelles sensationnelles mais encore insuffisamment vérifiées, ou bien déformées. Nulle planète n'a encore pu être photographiée directement, contrairement à ce que l'on a quelques temps pensé en 1998... la planète prétendument "éjectée" par son étoile s'est avérée finalement n'être qu'une banale étoile lointaine! On n'a pas encore découvert de planète semblable à la nôtre, contrairement à ce qui a parfois été insinué : on a bien mis en évidence la présence de sodium dans l'atmosphère d'une planète géante extrêmement chaude (température de l'ordre de 1000K), mais cette planète ne peut en aucun cas être confondue avec une jumelle de la Terre!! Cependant, les découvertes effectivement faites depuis 1992 sont considérables, et les perspectives d'avenir permettent d'envisager ce genre de découvertes dans les 20 ans qui viennent... Les projets en cours ne découvriront peut-être pas de vie "semblable" à celle qui existe sur notre planète, mais ils ont tout au moins l'ambition de pouvoir apporter une réponse, négative ou positive, à cette question.